
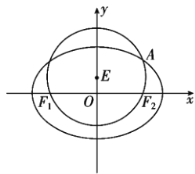
【题目】如图,已知圆![]() :
: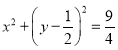 经过椭圆
经过椭圆![]() :
:![]() (
(![]() )的左右焦点
)的左右焦点![]() ,
,![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设与直线![]() (
(![]() 为原点)平行的直线
为原点)平行的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.当
两点.当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)由![]() ,
,![]() ,
,![]() 三点共线可知
三点共线可知![]() 为圆
为圆![]() 的直径,从而可得
的直径,从而可得![]() ,在圆方程中令
,在圆方程中令![]() 求出
求出![]() 即
即![]() ,由勾股定理可求得
,由勾股定理可求得![]() ,由椭圆定义求出
,由椭圆定义求出![]() 的值即可;(Ⅱ)设直线
的值即可;(Ⅱ)设直线![]() 的方程为
的方程为![]() ,联立方程组,由弦长公式求出
,联立方程组,由弦长公式求出![]() ,由点到直线的距离公式求出
,由点到直线的距离公式求出![]() 到直线
到直线![]() 的距离
的距离![]() ,求出三角形面积表达式
,求出三角形面积表达式![]() ,由基本不等式求最值及取得最值时
,由基本不等式求最值及取得最值时![]() 的值即可.
的值即可.
试题解析:(Ⅰ)![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 为圆
为圆![]() 的直径,且
的直径,且![]() ,
,
![]() .
.
由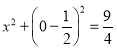 ,
,
得![]() ,
,
![]() …(2分)
…(2分)
![]() ,
,![]()
![]() ,
,![]() .(3分)
.(3分)
![]() ,
,![]() ,………(4分)
,………(4分)
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .…(5分)
.…(5分)
(Ⅱ)由(Ⅰ)知,点![]() 的坐标为
的坐标为![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() (6分)
(6分)
故设直线![]() 的方程为
的方程为![]() ,
,
联立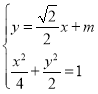 得,
得,![]() …………(7分)
…………(7分)
设![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .……(8分)
.……(8分)
又![]()
![]() ……(9分)
……(9分)
![]() 点
点![]() 到直线
到直线![]() 的距离
的距离![]() (10分)
(10分)
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
此时直线![]() 的方程为
的方程为![]() .…………(12分)
.…………(12分)


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知a是实数,函数f(x)=![]() (x-a).
(x-a).
(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数![]() ≤3;②标准差S≤2;③平均数
≤3;②标准差S≤2;③平均数![]() ≤3且标准差S≤2;④平均数
≤3且标准差S≤2;④平均数![]() ≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
A.①② B.③④
C.③④⑤ D.④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知底角为45的等腰梯形ABCD,底边BC长为7cm,腰长为![]() ,当一条垂直于底边BC
,当一条垂直于底边BC
(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x
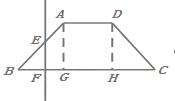
(1)试写出直线l左边部分的面积f(x)与x的函数.
(2)已知A={x|f(x)<4},B={x|a2<x<a+2},若A∪B=B,求a的取值范围。.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为![]() .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点且
两点且![]() ,是否存在以原点
,是否存在以原点![]() 为圆心的定圆与直线
为圆心的定圆与直线![]() 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos xsin 2x,下列结论中正确的是________(填入正确结论的序号).
①y=f(x)的图象关于点(2π,0)中心对称;
②y=f(x)的图象关于直线x=π对称;
③f(x)的最大值为![]() ;
;
④f(x)既是奇函数,又是周期函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2-xlna,a>1.
(1)求证:函数f(x)在(0,+∞)上单调递增;
(2)对任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤e-1恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com