
【题目】已知椭圆![]() 的一个顶点是
的一个顶点是![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知矩形![]() 的四条边都与椭圆
的四条边都与椭圆![]() 相切,设直线AB方程为
相切,设直线AB方程为![]() ,求矩形
,求矩形![]() 面积的最小值与最大值.
面积的最小值与最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时S有最大值10;当k=0时,S有最小值8.
时S有最大值10;当k=0时,S有最小值8.
【解析】
试题(Ⅰ)利用待定系数法即可,由题意,椭圆![]() 的一个顶点是
的一个顶点是![]() ,
,
所以![]() ,又
,又![]()
![]()
![]() ,椭圆C的方程是
,椭圆C的方程是![]() ;(Ⅱ)注意斜率的讨论,当
;(Ⅱ)注意斜率的讨论,当![]() 时,
时,
椭圆的外切矩形![]() 面积为8. 当
面积为8. 当![]() 时, AB所在直线方程为
时, AB所在直线方程为![]() ,所以,直线BC和AD的斜率均为
,所以,直线BC和AD的斜率均为![]() .联立直线AB与椭圆方程可得
.联立直线AB与椭圆方程可得![]() ,令
,令![]() 得到
得到![]() ,直线AB与直线DC之间的距离为
,直线AB与直线DC之间的距离为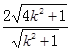 ,同理可求BC与AD距离为
,同理可求BC与AD距离为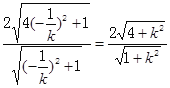 ,所以矩形ABCD的面积为
,所以矩形ABCD的面积为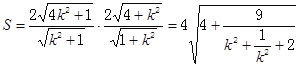 ,再利用基本不等式即可解决.
,再利用基本不等式即可解决.
试题解析:(Ⅰ)由题意,椭圆![]() 的一个顶点是
的一个顶点是![]() ,
,
所以![]()
又,离心率为![]() ,即
,即![]() ,
,![]()
解得![]() ,
,
故椭圆C的方程是![]()
(Ⅱ)当![]() 时,
时,
椭圆的外切矩形![]() 面积为8.
面积为8.
当![]() 时,
时,
椭圆的外切矩形![]() 的边AB所在直线方程为
的边AB所在直线方程为![]() ,
,
所以,直线BC和AD的斜率均为![]() .
.
由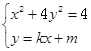 ,消去y得
,消去y得
![]() ,
,![]()
化简得:![]()
所以,直线AB方程为![]()
直线DC方程为![]()
直线AB与直线DC之间的距离为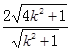
同理,可求BC与AD距离为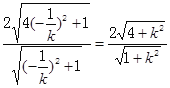
则矩形ABCD的面积为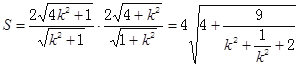
由均值定理![]()
仅当![]() ,即
,即![]() 时S有最大值10.
时S有最大值10.
因此,当![]() 时S有最大值10;
时S有最大值10;
当K=0时,S有最小值8.


科目:高中数学 来源: 题型:
【题目】已知点![]() 和椭圆
和椭圆![]() . 直线
. 直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(Ⅰ) 求椭圆![]() 的离心率;
的离心率;
(Ⅱ) 当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,当
,当![]() 为
为![]() 中点时,求
中点时,求![]() 的值 .
的值 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点为
的两焦点为![]() ,
,![]() ,且过点
,且过点![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 不过点
不过点![]() 且不平行于坐标轴,记线段
且不平行于坐标轴,记线段![]() 的中点为
的中点为![]() ,求证:直线
,求证:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(3)若直线![]() 过点
过点![]() ,求
,求![]() 面积的最大值,以及取最大值时直线
面积的最大值,以及取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=![]() ,则下列结论中正确的序号是_____.
,则下列结论中正确的序号是_____.

①AC⊥BE ②EF∥平面ABCD ③△AEF的面积与△BEF的面积相等.④三棱锥A﹣BEF的体积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
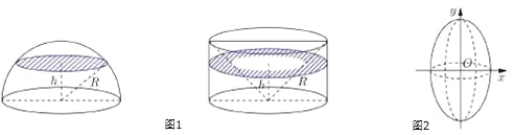
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图给出的是某高校土木工程系大四年级55名学生期末考试专业成绩的频率分布折线图(连接频率分布直方图中各小长方形上端的中点),其中组距为10,且本次考试中最低分为50分,最高分为100分.根据图中所提供的信息,则下列结论中正确的是( )
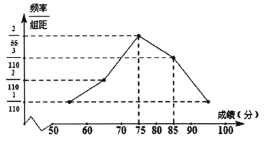
A. 成绩是75分的人数有20人
B. 成绩是100分的人数比成绩是50分的人数多
C. 成绩落在70-90分的人数有35人
D. 成绩落在75-85分的人数有35人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从10种不同的作物种子中选出6种分别放入6个不同的瓶子中,每瓶不空,如果甲、乙两种种子都不许放入第一号瓶子内,那么不同的放法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com