
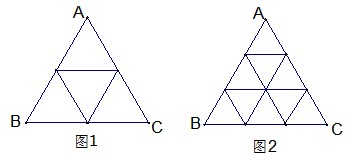
将正△ABC分割成n2(n≥2,n∈N)个全等的小正三角形(图乙,图丙分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于△ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别成等差数列,若顶点A,B,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,求f(3)和f(n).

解析:当n=3时,如题图所示分别设各顶点的数用小写字母表示,即由条件知
a+b+c=1,x1+x2=a+b,y1+y2=b+c,z1+z2=c+a.
x1+x2+y1+y2+z1+z2=2(a+b+c)=2,
2g=x1+y2=x2+z1=y1+z2.
6g=x1+x2+y1+y2+z1+z2=2(a+b+c)=2.
即g=而f(3)=a+b+c+x1+x2+y1+y2+z1+z2+g=
1+2+=.
进一步可求得f(4)=5.由上知f(1)中有三个数,f(2)中有6个数,f(3)中共有10个数相加,f(4)中有15个数相加…,若f(n-1)中有an-1(n>1)个数相加,可得f(n)中有(an-1+n+1)个数相加,且由f(1)=1=,f(2)===f(1)+,f(3)==f(2)+,f(4)=5=f(3)+,…
可得f(n)=f(n-1)+,所以
f(n)=f(n-1)+=f(n-2)++=…
=++++f(1)
=+++++=(n+1)(n+2).
【解析】略


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009湖南卷理)将正ABC分割成![]()
![]() (
(![]() ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= ,…,
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= ,…,

查看答案和解析>>
科目:高中数学 来源: 题型:
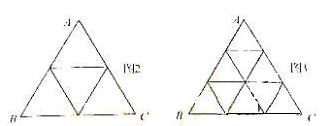
将正⊿ABC分割成![]()
![]() (
(![]() ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= ,…,f(n)=
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= ,…,f(n)=

查看答案和解析>>
科目:高中数学 来源: 题型:
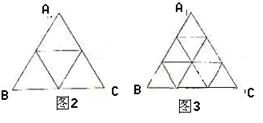
将正⊿ABC分割成![]()
![]() (
(![]() ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)=
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= ![]() ,…,f(n)=
,…,f(n)= ![]() (n+1)(n+2)
(n+1)(n+2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com