
某工厂生产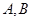 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
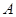 | 7 | 7 | 7.5 | 9 | 9.5 |
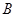 | 6 | 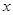 | 8.5 | 8.5 |  |
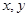 看不清,统计员只记得
看不清,统计员只记得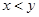 ,且
,且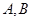 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.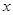 与
与 的值;
的值;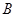 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. (Ⅰ)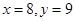 ;(Ⅱ)
;(Ⅱ)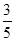
解析试题分析:(Ⅰ) 根据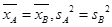 列方程组解
列方程组解 的值;(Ⅱ)由(Ⅰ)的结果知,被检测的5件
的值;(Ⅱ)由(Ⅰ)的结果知,被检测的5件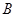 种元件,其中只有一件是次品,从中任取两件,列举出所有的基本结果,从中找出两件都是正品的基本结果的个数,由于是任意抽取的,每个结果出现的可能性是相等的,故可根据古典概型求2件都为正品的概率.
种元件,其中只有一件是次品,从中任取两件,列举出所有的基本结果,从中找出两件都是正品的基本结果的个数,由于是任意抽取的,每个结果出现的可能性是相等的,故可根据古典概型求2件都为正品的概率.
试题解析:(Ⅰ)因为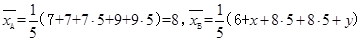 ,
,
由 ,得
,得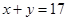 . ① 2分
. ① 2分
因为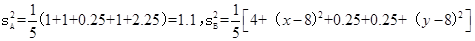 ,
,
由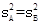 ,得
,得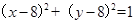 . ② 4分
. ② 4分
由①②解得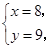 或
或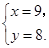 ,因为
,因为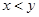 ,所以
,所以 . 6分
. 6分
(Ⅱ)记被检测的5件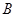 种元件分别为
种元件分别为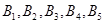 ,其中
,其中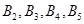 为正品,
为正品,
从中任取2件,共有10个基本事件,列举如下: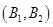 ,
,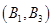 ,
,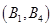 ,
,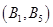 ,
,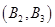 ,
,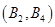 ,
,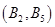 ,
,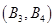 ,
, ,
,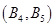 , 8分
, 8分
记“2件都为正品”为事件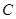 ,则事件
,则事件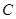 包含以下6个基本事件:
包含以下6个基本事件: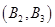 ,
,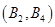 ,
,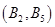 ,
,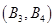 ,
, ,
,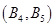 . 10分
. 10分
所以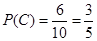 ,即2件都为正品的概率为
,即2件都为正品的概率为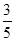 . 12分
. 12分
考点:1、样本均值、方差公式;2、古典概型.


科目:高中数学 来源: 题型:解答题
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 =bx+a.
=bx+a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组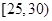 ,第2组
,第2组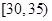 ,第3组
,第3组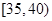 ,第4组
,第4组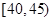 ,第5组
,第5组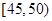 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.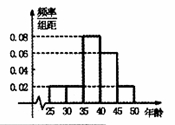

(1)求正整数 的值;
的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
 .
.| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| K | 2.706 | 3.841 | 60635 | 7.879 |
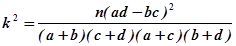 )其中n=a+b+c+d
)其中n=a+b+c+d查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班高一某班的一次数学测试成绩的茎叶图和频率分布图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
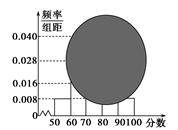
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据空气质量指数 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
 (数值) (数值) | 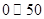 | 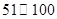 |  |  |  |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
 年
年 月
月 日—
日— 月
月 日,对空气质量指数
日,对空气质量指数 进行监测,获得数据后得到如图的条形图
进行监测,获得数据后得到如图的条形图
 天计)空气质量类别为中度污染的概率;
天计)空气质量类别为中度污染的概率; 个监测数据中任取
个监测数据中任取 个,设
个,设 为空气质量类别颜色为紫色的天数,求
为空气质量类别颜色为紫色的天数,求 的分布列.
的分布列.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某电子元件进行寿命追踪调查,所得情况如下频率分布直方图.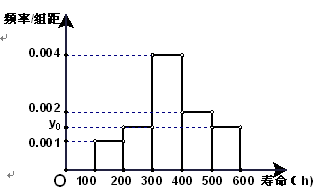
(1)图中纵坐标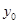 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原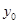 ;
;
(2)根据图表的数据按分层抽样,抽取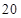 个元件,寿命为
个元件,寿命为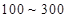 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在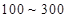 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为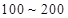 ,一个寿命为
,一个寿命为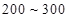 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在2012年“双节”期间,高速公路车辆较多。某调查公司在一服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽取一辆的抽样方法,抽取了40名驾驶员进行调查,将他们在某段高速公路上的车速(km/t)分成6段: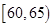 ,
, ,
, ,
, ,
, ,
, 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
(1)该公司在调查取样中,用到的是什么抽样方法?
(2)求这40辆小型汽车车速的众数和中位数的估计值;
(3)若从车速在 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 中的车辆数
中的车辆数 的分布列及其数学期望。(12分)
的分布列及其数学期望。(12分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
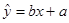 ;
;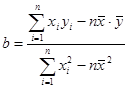 ,
, )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com