
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形,![]() ,
,![]() .
.
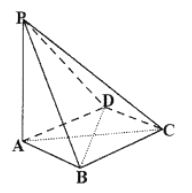
(1)若![]() ,求
,求![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)当平面![]() 与平面
与平面![]() 垂直时,求
垂直时,求![]() 的长.
的长.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)结合已知条件,设![]() 与
与![]() 的交点为
的交点为![]() ,则
,则![]() ,故考虑分别以
,故考虑分别以![]() 为
为![]() 轴、
轴、![]() 轴,以过
轴,以过![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() 与
与![]() 所成的角为
所成的角为![]() ,则
,则![]() 可转化为
可转化为![]() 与
与![]() 所成的角,代入公式
所成的角,代入公式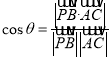 可求;(2)分别求平面
可求;(2)分别求平面![]() 的法向量,平面
的法向量,平面![]() 的法向量,由平面
的法向量,由平面![]() 平面
平面![]() 可得
可得![]() 从而可求
从而可求![]() 即
即![]() .
.
试题解析:(1)因为四边形![]() 是菱形,所以
是菱形,所以![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
设![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
如图,以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
设![]() 与
与![]() 所成角为
所成角为![]() ,则
,则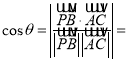
![]() .
.
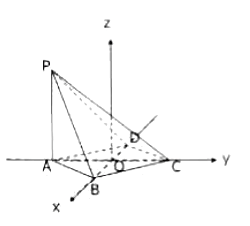
(2)由(1)知![]() ,设
,设![]() (
(![]() ),则
),则![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则![]() ,
,![]() ,所以
,所以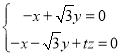 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() .
.
同理,平面![]() 的法向量
的法向量![]() .
.
因为平面![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() .所以
.所以![]() .
.
【方法点晴】本题主要考查利用空间向量求异面直线成的角,以及向量垂直的应用,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次人才招聘会上,有![]() 、
、![]() 两家公司分别开出了他们的工资标准:
两家公司分别开出了他们的工资标准:![]() 公司允诺第一个月工资为8000元,以后每年月工资比上一年月工资增加500元;
公司允诺第一个月工资为8000元,以后每年月工资比上一年月工资增加500元;![]() 公司允诺第一年月工资也为8000元,以后每年月工资在上一年的月工资基础上递增
公司允诺第一年月工资也为8000元,以后每年月工资在上一年的月工资基础上递增![]() ,设某人年初被
,设某人年初被![]() 、
、![]() 两家公司同时录取,试问:
两家公司同时录取,试问:
(1)若该人分别在![]() 公司或
公司或![]() 公司连续工作
公司连续工作![]() 年,则他在第
年,则他在第![]() 年的月工资分别是多少;
年的月工资分别是多少;
(2)该人打算连续在一家公司工作10年,仅从工资收入总量较多作为应聘的标准(不计其他因素),该人应该选择哪家公司,为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设递增数列![]() 共有
共有![]() 项,定义集合
项,定义集合![]() ,将集合
,将集合![]() 中的数按从小到大排列得到数列
中的数按从小到大排列得到数列![]() ;
;
(1)若数列![]() 共有4项,分别为
共有4项,分别为![]() ,
,![]() ,
,![]() ,
,![]() ,写出数列
,写出数列![]() 的各项的值;
的各项的值;
(2)设![]() 是公比为2的等比数列,且
是公比为2的等比数列,且![]() ,若数列
,若数列![]() 的所有项的和为4088,求
的所有项的和为4088,求![]() 和
和![]() 的值;
的值;
(3)若![]() ,求证:
,求证:![]() 为等差数列的充要条件是数列
为等差数列的充要条件是数列![]() 恰有7项;
恰有7项;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com