
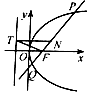
 如图所示,抛物线C:y2=2px(p>0)的焦点为F,经过点F的直线l与抛物线交于P,Q两点,弦PQ的中点为N,经过点N作y轴的垂线与C的准线交于点T.
如图所示,抛物线C:y2=2px(p>0)的焦点为F,经过点F的直线l与抛物线交于P,Q两点,弦PQ的中点为N,经过点N作y轴的垂线与C的准线交于点T.分析 (Ⅰ)设直线l的方程为y=x-$\frac{p}{2}$,与抛物线C的方程联立,化简得x2-3px+$\frac{{p}^{2}}{4}$=0,根据|PQ|=4,求抛物线C的标准方程;
(Ⅱ)求出点N、点T的坐标,证明$\overrightarrow{FT}$•$\overrightarrow{FN}$=-p2m2+p2m2=0,即可证明:无论p为何值,以线段TN为直径的圆总经过点F.
解答 (Ⅰ)解:由直线l的斜率为1,可设直线l的方程为y=x-$\frac{p}{2}$,
与抛物线C的方程联立,化简得x2-3px+$\frac{{p}^{2}}{4}$=0,
设P(x1,y1),Q(x2,y2),由韦达定理可知,x1+x2=3p,
∴|PQ|=x1+x2+p=4p=4,p=1,
∴抛物线C的方程为y2=2x.…(5分)
(Ⅱ)证明:设直线l的方程为x=my+$\frac{p}{2}$,
与抛物线C的方程联立,化简得y2-2pmy-p2=0,
设P(x1,y1),Q(x2,y2),由韦达定理可知,y1+y2=2pm,
∴x1+x2=m(y1+y2)+p=2pm2+p,
∴点N的坐标为(pm2+$\frac{p}{2}$,pm),
∴点T的坐标为(-$\frac{p}{2}$,pm),
∴$\overrightarrow{FT}$=(-p,pm),$\overrightarrow{FN}$=(pm2,pm),
∴$\overrightarrow{FT}$•$\overrightarrow{FN}$=-p2m2+p2m2=0,
∴无论p为何值,以线段TN为直径的圆总经过点F.…(12分)
点评 本题考查抛物线的标准方程,考查直线与抛物线的位置关系,同时考查向量与解析几何的交汇,综合性强.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | x2-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-y2=1 | C. | $\frac{{y}^{2}}{16}$-x2=1 | D. | y2-$\frac{{x}^{2}}{16}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cosx | B. | y=-x2 | C. | $y={(\frac{1}{2})^{|x|}}$ | D. | y=|sinx| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2} | B. | {-1,0,1} | C. | {-3,-2,-1,0,1,2} | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ②③ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com