
y 人数 x | 价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服 务 满 意 度 | 1 | 1 | 1 | 2 | 2 | 0 |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 0 | 1 | 2 | 3 | 1 | |
分析 (Ⅰ)利用统计结果能作出“价格满意度”的频率分布直方图.
(Ⅱ)x<3且y<3的五人中,有2人“服务满意度”为1,有3人“服务满意度”为2,从中抽取两人,基本事件总数n=${C}_{5}^{2}=10$,至少有一人的“服务满意度”为1的对立事件是抽取的2人的“服务满意度”都为2,由此利用对立事件概率计算公式能求出至少有一人的“服务满意度”为1的概率.
解答 解:(Ⅰ)“价格满意度”的频率分布直方图如下图所示: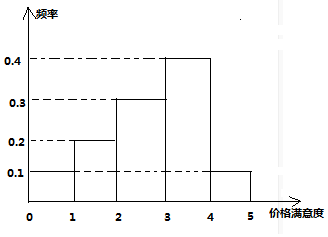
(Ⅱ)x<3且y<3的五人中,
有2人“服务满意度”为1,有3人“服务满意度”为2,
从中抽取两人,基本事件总数n=${C}_{5}^{2}=10$,
至少有一人的“服务满意度”为1的对立事件是抽取的2人的“服务满意度”都为2,
∴至少有一人的“服务满意度”为1的概率:
p=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{7}{10}$.
点评 本题考查频率分布直方图的作法,考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
 如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,则|$\overrightarrow{OA}$+$\overrightarrow{OP}$|的取值范围为( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,则|$\overrightarrow{OA}$+$\overrightarrow{OP}$|的取值范围为( )| A. | [$\frac{2\sqrt{10}}{5}$,5] | B. | [$\sqrt{2}$,4] | C. | [$\sqrt{2}$,$\sqrt{5}$] | D. | [$\frac{2\sqrt{10}}{5}$,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2018 | B. | 2017 | C. | 2016 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2$\sqrt{2}$ | C. | 16 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
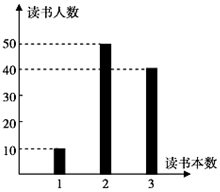 某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.
某校开展“读好书,好读书”活动,要求本学期每人至少读一本课外书,该校高一共有100名学生,他们本学期读课外书的本数统计如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com