
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.
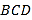
(1)证明:![]() 平面
平面![]() ;
;
(2)过点![]() 作一平行于平面
作一平行于平面![]() 的截面,画出该截面,说明理由,并求夹在该截面与平面
的截面,画出该截面,说明理由,并求夹在该截面与平面![]() 之间的几何体的体积.
之间的几何体的体积.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 相邻两个最高点的距离等于
相邻两个最高点的距离等于![]() .
.
(1)求![]() 的值;
的值;
(2)求出函数![]() 的对称轴,对称中心;
的对称轴,对称中心;
(3)把函数![]() 图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),得到函数
图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),得到函数![]() ,再把函数
,再把函数![]() 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() ,不需要过程,直接写出函数
,不需要过程,直接写出函数![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中数列
,其中数列![]() 是公比为
是公比为![]() 的等比数列,数列
的等比数列,数列![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(1)若![]() ,
,![]() ,分别写出数列
,分别写出数列![]() 和数列
和数列![]() 的通项公式;
的通项公式;
(2)若![]() 是奇函数,且
是奇函数,且![]() ,求
,求![]() ;
;
(3)若函数![]() 的图像关于点
的图像关于点![]() 对称,且当
对称,且当![]() 时,函数
时,函数![]() 取得最小值,求
取得最小值,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:

(1)现要在这10户家庭中任意选取3家,求取到第二阶梯水量的户数![]() 的分布列与数学期望;
的分布列与数学期望;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为二阶的可能性最大,求
户月用水量为二阶的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三角形面积为![]() ,
,![]() ,
,![]() ,
,![]() 为三角形三边长,
为三角形三边长,![]() 为三角形内切圆半径,利用类比推理,可以得出四面体的体积为( )
为三角形内切圆半径,利用类比推理,可以得出四面体的体积为( )
A. ![]()
B. ![]()
C. ![]() (
(![]() 为四面体的高)
为四面体的高)
D. ![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 分别为四面体四个面的面积,
分别为四面体四个面的面积,![]() 为四面体内切球的半径,设四面体的内切球的球心为
为四面体内切球的半径,设四面体的内切球的球心为![]() ,则球心
,则球心![]() 到四个面的距离都是
到四个面的距离都是![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年3月3日至20日中华人民共和国第十三届全国人民代表大会第一次会议和中国人民政治协商会议第十三届全国委员会第一次会议在北京胜利召开,两会是年度中国政治生活中的一件大事,受到了举国上下和全世界的广泛关注.为及时宣传国家政策,贯彻两会精神,某校举行了全国两会知识竞赛,为了解本次竞赛成绩情况,随机抽取了部分学生的成绩(得分均为整数,满分![]() 分,最低分不低于
分,最低分不低于![]() 分)进行统计,得出频率分布表如下:
分)进行统计,得出频率分布表如下:
组号 | 分组 | 频数 | 频率 |
第1组 |
|
|
|
第2组 |
|
|
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
合计 |
|
| |
(1)求表中![]() 、
、![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若从成绩较好的第![]() 、
、![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人担任两会知识宣传员,再从这
人担任两会知识宣传员,再从这![]() 人中随机选出
人中随机选出![]() 人负责整理两会相关材料,求这
人负责整理两会相关材料,求这![]() 人中至少有
人中至少有![]() 人来自第
人来自第![]() 组的概率.
组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com