练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数 .
    （1）证明 有且只有一个零点；
    （2）求这个零点所在的一个区间，使这个区间的长度不大于 .

    【答案】
    （1）证明：易知f(x)＝lnx＋2x6在(0，＋∞)上是增函数，
    ∴f(x)至多有一个零点．由于f(2)＝ln22<0，f(3)＝ln3>0，
    ∴f(2)·f(3)<0. ∴f(x)在(2，3)内有一个零点．∴f(x)在(0，＋∞)上只有一个零点
    （2）解：由(1)知f(2)<0，f(3)>0，取 ， ，
    ∴ .∴ 的零点 ．取 ，
    则 .
    ∴ .∴ ．
    ∵ ，∴满足题意的区间为
    【解析】(1)递增函数在某个区间中最多一个零点,而函数的端点处函数值异号时,则有且只有一个零点;
    (2)结合二分法及精确度的要求,可求出对应区间.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知{an}是等差数列，{bn}是等比数列，且b2=3，b3=9，a1=b1 ， a14=b4 ．
    （1）求{an}的通项公式；
    （2）设cn=an+bn ， 求数列{cn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了得到函数y=sin（2x+ ）的图象，只需将y=cos2x的图象上每一点（ ）
    A.向右平移 个单位长度
    B.向右平移 个单位长度
    C.向左平移 个单位长度
    D.向左平移 个单位长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}前n项的和为Sn ， 满足a1=0，an≥0，3an+12=an2+an+1（n∈N*） （Ⅰ）用数学归纳法证明：1 ≤an＜1（n∈N*）
    （Ⅱ）求证：an＜an+1（n∈N*）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某种水箱用的“浮球”，是由两个半球和一个圆柱筒组成的．已知半球的直径是6 cm，圆柱筒高为2 cm.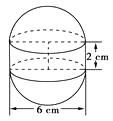

    （1）这种“浮球”的体积是多少cm3（结果精确到0.1）?
    （2）要在2 500个这样的“浮球”表面涂一层胶，如果每平方米需要涂胶100克，那么共需胶多少克？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x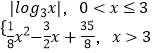）= ，若函数g（x）=f（x）﹣m存在4个不同的零点x1 ， x2 ， x3 ， x4 ， 则实数m的取值范围是 ， x1x2x3x4的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥 的底面为正方形，侧面 底面 ， ， 分别为 的中点.

    （1）求证： 面 ；
    （2）求证：平面 平面 .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x+ ﹣3lnx（a∈R）．
    （1）若x=3是f（x）的一个极值点，求a值及f（x）的单调区间；
    （2）当a=﹣2时，求f（x）在区间[1，e]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动圆 经过点 ， .
    （1）求周长最小的圆的一般方程；
    （2）求圆心在直线 上的圆的标准方程.

    查看答案和解析>>

    同步练习册答案