
【题目】已知函数f (x)=ln x+x2-ax(a为常数).
(1)若x=1是函数f (x)的一个极值点,求a的值;
(2)当0<a≤2时,试判断f (x)的单调性;
(3)若对任意的a∈(1,2),x0∈[1,2],不等式f (x0)>mln a 恒成立,求实数m的取值范围.
【答案】(1)3;(2)见解析;(3)![]()
【解析】试题分析:(1)求出![]() ,由
,由![]() 列方程即可求
列方程即可求![]() 的值;(2)求出
的值;(2)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;;(3)问题等价于:对任意的
的减区间;;(3)问题等价于:对任意的![]() ,不等式
,不等式![]() 恒成立,即
恒成立,即![]() 恒成立,利用导数研究函数的单调性,根单调性求出
恒成立,利用导数研究函数的单调性,根单调性求出![]() 的最小值,进而可得结果.
的最小值,进而可得结果.
试题解析: f ′(x)=![]() +2x-a.
+2x-a.
(1)由已知得:f ′(1)=0,所以1+2-a=0,所以a=3,经验证符合题意.
(2)当0<a≤2时,f ′(x)=![]() +2x-a=
+2x-a=![]()
=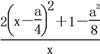 .
.
因为0<a≤2,所以1-![]() >0,而x>0,
>0,而x>0,
即f ′(x)=![]() >0,
>0,
故f (x)在(0,+∞)上是增函数.
(3)当a∈(1,2)时,由(2)知,f (x)在[1,2]上的最小值为f (1)=1-a,
故问题等价于:对任意的a∈(1,2),
不等式1-a>mln a恒成立,即m<![]() 恒成立.
恒成立.
记g(a)=![]() (1<a<2),则g′(a)=
(1<a<2),则g′(a)=![]() .
.
令M(a)=-aln a-1+a,则M′(a)=-ln a<0,
所以M(a)在(1,2)上单调递减,
所以M(a)<M(1)=0,故g′(a)<0,
所以g(a)=![]() 在a∈(1,2)上单调递减,
在a∈(1,2)上单调递减,
所以m≤g(2)=![]() =-log2e,
=-log2e,
即实数m的取值范围为(-∞,-log2e].


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】定义满足不等式|x![]() A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b
A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b![]() t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)对任意实数x、y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=-![]() .
.
(1)求证:f(x)为奇函数;
(2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. ![]() 是向量
是向量![]() ,
,![]() 不共线的充要条件
不共线的充要条件
B. 在空间四边形![]() 中,
中,![]()
C. 在棱长为1的正四面体![]() 中,
中,![]()
D. 设![]() ,
,![]() ,
,![]() 三点不共线,
三点不共线,![]() 为平面
为平面![]() 外一点,若
外一点,若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面
四点共面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 在抛物线
在抛物线![]() 外,过点
外,过点![]() 作抛物线
作抛物线![]() 的两切线,设两切点分别为
的两切线,设两切点分别为![]() ,
,![]() ,记线段
,记线段![]() 的中点为
的中点为![]() .
.

(Ⅰ)求切线![]() ,
,![]() 的方程;
的方程;
(Ⅱ)证明:线段![]() 的中点
的中点![]() 在抛物线
在抛物线![]() 上;
上;
(Ⅲ)设点![]() 为圆
为圆![]() 上的点,当
上的点,当![]() 取最大值时,求点
取最大值时,求点![]() 的纵坐标.
的纵坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年10月9日,教育部考试中心下发了《关于2017年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.宿州市教育部门积极回应,编辑传统文化教材,在全市范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民120人中持支持态度的为80人.
,在抽取的男性市民120人中持支持态度的为80人.
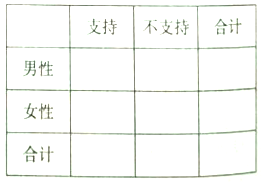
(Ⅰ)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?
(Ⅱ)为了进一步征求对开展传统文化的意见和建议,从抽取的200位市民中对不支持的按照分层抽样的方法抽取5位市民,并从抽取的5人中再随机选取2人进行座谈,求选取的2人恰好为1男1女的概率.
附: 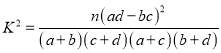 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,其左焦点与抛物线
,其左焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)过动点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,
,![]() 在第一象限,
在第一象限,![]() ,过点
,过点![]() 做
做![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() ,连接
,连接![]() 并延长交椭圆
并延长交椭圆![]() 于另一点
于另一点![]() .设直线
.设直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明:![]() 为定值.
为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且![]() ,若任意的
,若任意的![]() ,当
,当![]() 时,总有
时,总有![]() .
.
(1)判断函数![]() 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式:![]() ;
;
(3)若![]() 对所有的
对所有的![]() 恒成立,其中
恒成立,其中![]() (
(![]() 是常数),求实数
是常数),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com