
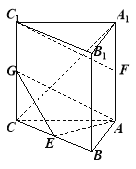
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,
的中点,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() //平面
//平面![]() .
.
(1)求![]() 的值;
的值;
(2)求证:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)详见解析;(3)二面角
;(2)详见解析;(3)二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】
试题分析:(1)求![]() 的值,关键是找
的值,关键是找![]() 在
在![]() 的位置,注意到
的位置,注意到![]() 平面
平面![]() ,有线面平行的性质,可得
,有线面平行的性质,可得![]() ,由已知
,由已知![]() 为
为![]() 中点,由平面几何知识可得
中点,由平面几何知识可得![]() 为
为![]() 中点,从而可得
中点,从而可得![]() 的值;(2)求证:
的值;(2)求证:![]() ,有图观察,用传统方法比较麻烦,而本题由于
,有图观察,用传统方法比较麻烦,而本题由于![]() 底面
底面![]() ,所以
,所以![]() ,
,![]() ,又
,又![]() ,这样建立空间坐标比较简单,故以
,这样建立空间坐标比较简单,故以![]() 为原点,以
为原点,以![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,取
,取![]() ,可写出个点坐标,从而得向量
,可写出个点坐标,从而得向量![]() 的坐标,证
的坐标,证![]() 即可;(3)求二面角
即可;(3)求二面角![]() 的余弦值,由题意可得向量
的余弦值,由题意可得向量![]() 是平面
是平面![]() 的一个法向量,只需求出平面
的一个法向量,只需求出平面![]() 的一个法向量,可设平面
的一个法向量,可设平面![]() 的法向量
的法向量![]() ,利用
,利用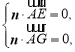 ,即可求出平面
,即可求出平面![]() 的一个法向量,利用向量的夹角公式即可求出二面角
的一个法向量,利用向量的夹角公式即可求出二面角![]() 的余弦值.
的余弦值.
(1)因为![]() 平面
平面![]()
又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() . 3分
. 3分
因为![]() 为
为![]() 中点,且侧面
中点,且侧面![]() 为平行四边形
为平行四边形
所以![]() 为
为![]() 中点,所以
中点,所以![]() . 4分
. 4分
(2)因为![]() 底面
底面![]() ,
,
所以![]() ,
,![]() , 5分
, 5分
又![]() ,
,
如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,设
,设![]() ,则由
,则由![]() 可得
可得![]() 6分
6分
因为![]() 分别是
分别是![]() 的中点,
的中点,
所以![]() . 7分
. 7分
![]() . 8分
. 8分
所以![]() ,
,
所以![]() . 9分
. 9分

(3)设平面![]() 的法向量
的法向量![]() ,则
,则
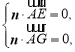 即
即![]() 10分
10分
令![]() ,则
,则![]() ,所以
,所以![]() . 11分
. 11分
由已知可得平面![]() 的法向量
的法向量![]() 11分
11分
所以![]() 13分
13分
由题意知二面角![]() 为钝角,
为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]() . 14分
. 14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.
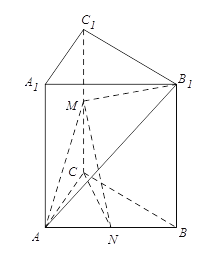
(1)求证:CN⊥平面ABB1A1;
(2)求证:CN∥平面AMB1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 分别为
分别为![]() 与
与![]() 轴,
轴, ![]() 轴的交点.
轴的交点.
(1)写出![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 的极坐标;
的极坐标;
(2)设![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]() ,由
,由![]() 中的元素构成两个相应的集合:
中的元素构成两个相应的集合:
![]() ,
, ![]() .
.
其中![]() 是有序数对,集合
是有序数对,集合![]() 和
和![]() 中的元素个数分别为
中的元素个数分别为![]() 和
和![]() .
.
若对于任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(Ⅰ)检验集合![]() 与
与![]() 是否具有性质
是否具有性质![]() 并对其中具有性质
并对其中具有性质![]() 的集合,写出相应的集合
的集合,写出相应的集合![]() 和
和![]() .
.
(Ⅱ)对任何具有性质![]() 的集合
的集合![]() ,证明
,证明![]() .
.
(Ⅲ)判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的导函数为
的导函数为![]() .
.
⑴ 若直线![]() 与曲线
与曲线![]() 恒相切于同一定点,求
恒相切于同一定点,求![]() 的方程;
的方程;
⑵ 若![]() ,求证:当
,求证:当![]() 时,
时, ![]() 恒成立;
恒成立;
⑶ 若当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com