
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若方程![]() 没有实数解,求实数
没有实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() 在
在![]() 单调递减,
单调递减,![]() 在
在![]() 上单调递增;
上单调递增;
(II)![]()
【解析】
(I)先对函数求导,结合导数与单调性的关系即可求解函数的单调性;
(II)由![]() 没有实数解,结合a的范围,利用函数的单调性及函数的性质可判断函数的零点存在情况,即可求解.
没有实数解,结合a的范围,利用函数的单调性及函数的性质可判断函数的零点存在情况,即可求解.
(Ⅰ)当![]() 时,
时,![]() ,函数的定义域为
,函数的定义域为![]() ,
,
所以![]() ,
,
令![]() ,得
,得![]() ,
,
又因为函数![]() 单调递增,
单调递增,
所以在![]() 上,
上,![]() ,
,![]() 单调递减;
单调递减;
在![]() 上,
上,![]() ,
,![]() 单调递增.
单调递增.
(II)方程![]() 没有实数解,
没有实数解,
即方程![]() 没有实数解,
没有实数解,
设函数![]() ,
,
![]() ,
,
(i)当![]() 时,
时,![]() ,函数
,函数![]() 没有零点;
没有零点;
(ii)当![]() 时,函数
时,函数![]() 单调递减,
单调递减,![]() ,且
,且![]() ,函数
,函数![]() 有零点;
有零点;
(iii)当![]() 时,令
时,令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,
令![]() ,得
,得![]() ,
,
即函数![]() 没有零点,
没有零点,
综上所述,若函数![]() 没有零点,
没有零点,
即方程![]() 没有实数解,
没有实数解,
故实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】![]() 年,山东省高考将全面实行“
年,山东省高考将全面实行“![]() 选
选![]() ”的模式(即:语文、数学、外语为必考科目,剩下的物理、化学、历史、地理、生物、政治六科任选三科进行考试).为了了解学生对物理学科的喜好程度,某高中从高一年级学生中随机抽取
”的模式(即:语文、数学、外语为必考科目,剩下的物理、化学、历史、地理、生物、政治六科任选三科进行考试).为了了解学生对物理学科的喜好程度,某高中从高一年级学生中随机抽取![]() 人做调查.统计显示,男生喜欢物理的有
人做调查.统计显示,男生喜欢物理的有![]() 人,不喜欢物理的有
人,不喜欢物理的有![]() 人;女生喜欢物理的有
人;女生喜欢物理的有![]() 人,不喜欢物理的有
人,不喜欢物理的有![]() 人.
人.
(1)据此资料判断是否有![]() 的把握认为“喜欢物理与性别有关”;
的把握认为“喜欢物理与性别有关”;
(2)为了了解学生对选科的认识,年级决定召开学生座谈会.现从![]() 名男同学和
名男同学和![]() 名女同学(其中
名女同学(其中![]() 男
男![]() 女喜欢物理)中,选取
女喜欢物理)中,选取![]() 名男同学和
名男同学和![]() 名女同学参加座谈会,记参加座谈会的
名女同学参加座谈会,记参加座谈会的![]() 人中喜欢物理的人数为
人中喜欢物理的人数为![]() ,求
,求![]() 的分布列及期望
的分布列及期望![]() .
.
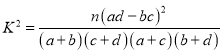 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于空间中的三条直线,有以下四个条件:①三条直线两两相交;②三条直线两两平行;③三条直线共点;④两直线相交,第三条平行于其中一条与另一条相交.其中使这三条直线共面的充分条件有______(填正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年第一期中国青年阅读指数数据显示,从阅读需求的角度,排名前三的阅读领域分别为文学、哲学及社会科学和历史.某学校从文科生和理科生中选取了经常阅读的学生进行了假期阅读内容和阅读时间方面的调查,得到以下数据.
学生所学文理与阅读内容列联表
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 70 | 130 | 200 |
文科生 | 45 | 55 | 100 |
合计 | 115 | 185 | 300 |
(Ⅰ)判断能否有![]() 把握认为学生所学文理与阅读内容有关?
把握认为学生所学文理与阅读内容有关?
(Ⅱ)从阅读时间大于30分钟的被调查同学中随机选取30名学生,其阅读时间(分钟)整理成如图所示的茎叶图,并绘制日均阅读时间分布表;
其中30名同学的日均阅读时间分布表(单位:分钟)
阅读时间 |
|
|
|
男生人数 | 4 |
| 2 |
女生人数 |
| 10 | 2 |
求出![]() ,
,![]() 的值,并根据日均时间分布表,估计这30名同学日阅读时间的平均值;
的值,并根据日均时间分布表,估计这30名同学日阅读时间的平均值;
(Ⅲ)从(Ⅱ)中日均阅读时间高于90分钟的同学中随机选取2人介绍阅读体会,求这2人性别相同的概率.
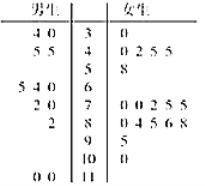
参考公式: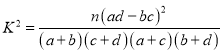 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“金镶玉”是北京奥运会的奖牌设计所采用的式样,喻示中国传统文化中的“金玉良缘”,体现了中国人对奥林匹克精神的礼赞和对运动员的褒奖.它的设计方案,创意十分新颖,突破了以往任何一届奥运会奖牌设计单一材质的传统,又融入了典型的中国文化元素,是中国文化与体育精神完美结合的载体.现有一矩形玉片![]() ,
,![]() 为
为![]() 毫米,
毫米,![]() 为32毫米,
为32毫米,![]() 为
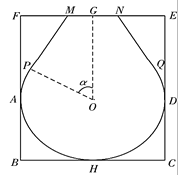
为![]() 的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧
的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧![]() 和线段
和线段![]() 其中优弧
其中优弧![]() 所在圆的圆心为
所在圆的圆心为![]() ,圆
,圆![]() 与矩形的边
与矩形的边![]() 分别相切于点
分别相切于点![]() 以及点
以及点![]() 在线段
在线段![]() 上(
上(![]() 在
在![]() 的左侧),
的左侧),![]() 分别于圆
分别于圆![]() 相切于点
相切于点![]() 且
且![]() .若优弧
.若优弧![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元(
元(![]() ),线段
),线段![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元.记锐角
元.记锐角![]() 镶嵌金丝的总造价为
镶嵌金丝的总造价为![]() 元.
元.
(1)试表示出关于![]() 的函数
的函数![]() 并写出
并写出![]() 的范围;
的范围;
(2)当镶嵌金丝的总造价最低时,求出四边形![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )经过点
)经过点![]() ,离心率为
,离心率为![]() ,
,![]() ,
,![]() 分别为椭圆的左、右焦点.
分别为椭圆的左、右焦点.
(1)求椭圆C的标准方程;
(2)若点![]() (
(![]() )在椭圆C上,求证;直线
)在椭圆C上,求证;直线![]() 与直线
与直线![]() 关于直线l:
关于直线l:![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在世界读书日期间,某地区调查组对居民阅读情况进行了调查,获得了一个容量为200的样本,其中城镇居民140人,农村居民60人.在这些居民中,经常阅读的城镇居民有100人,农村居民有30人.
(1)填写下面列联表,并判断能否有99%的把握认为经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 | 100 | 30 | |
不经常阅读 | |||
合计 | 200 |
(2)调查组从该样本的城镇居民中按分层抽样抽取出7人,参加一次阅读交流活动,若活动主办方从这7位居民中随机选取2人作交流发言,求被选中的2位居民都是经常阅读居民的概率.
附: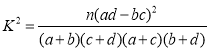 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com