
【题目】考前回归课本复习过程中,一数学老师在黑板上写了下面四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .然后说了四句话:第一句:“该函数定义域为
.然后说了四句话:第一句:“该函数定义域为![]() ,还是奇函数”.第二句:“该函数为偶函数,值域不是
,还是奇函数”.第二句:“该函数为偶函数,值域不是![]() ”.第三句:“该函数定义域为
”.第三句:“该函数定义域为![]() ,还是单调函数”.第四句:“该函数的图象有对称轴,值域是
,还是单调函数”.第四句:“该函数的图象有对称轴,值域是![]() ”,若老师的每一句话只说对了一半,则这四个函数中符合老师说的所有函数的编号为______________.
”,若老师的每一句话只说对了一半,则这四个函数中符合老师说的所有函数的编号为______________.
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(1)若![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 的斜率;
的斜率;
(2)若![]() ,且
,且![]() 的斜率为
的斜率为![]() ,当
,当![]() 时,求
时,求![]() 在
在![]() 轴上的截距的取值范围(用
轴上的截距的取值范围(用![]() 表示),并证明
表示),并证明![]() 的平分线始终与
的平分线始终与![]() 轴平行.
轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司以客户满意为出发点,随机抽选2000名客户,以调查问卷的形式分析影响客户满意度的各项因素.每名客户填写一个因素,下图为客户满意度分析的帕累托图.帕累托图用双直角坐标系表示,左边纵坐标表示频数,右边纵坐标表示频率,分析线表示累计频率,横坐标表示影响满意度的各项因素,按影响程度(即频数)的大小从左到右排列,以下结论正确的个数是( ).
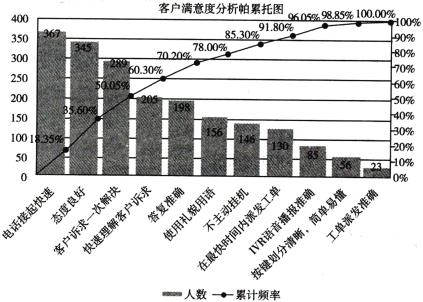
①35.6%的客户认为态度良好影响他们的满意度;
②156位客户认为使用礼貌用语影响他们的满意度;
③最影响客户满意度的因素是电话接起快速;
④不超过10%的客户认为工单派发准确影响他们的满意度.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,点
,点![]() ,
,![]() 在该抛物线上且位于
在该抛物线上且位于![]() 轴的两侧,
轴的两侧,![]() .
.
(Ⅰ)证明:直线![]() 过定点
过定点![]() ;
;
(Ⅱ)以![]() ,
,![]() 为切点作
为切点作![]() 的切线,设两切线的交点为
的切线,设两切线的交点为![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2![]() 。
。
(1)求椭圆的方程;
(2)如图,斜率为k的直线l过椭圆的右焦点F,且与椭圆交与A,B两点,以线段AB为直径的圆截直线x=1所得的弦的长度为![]() ,求直线l的方程。
,求直线l的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com