
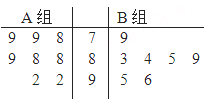
 天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.
天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.
| ||||
|
. |
| x |
| 78+79×3+83×2+84+85×2+88+89×2+92×2+95+96 |
| 16 |
| ||||
|
| 4 |
| 7 |
| ||||
|
| ||||
|
| 4 |
| 35 |
| ||||
|
| 18 |
| 35 |
| ||||
|
| 12 |
| 35 |
| ||||
|
| 1 |
| 35 |
| ζ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 4 |
| 35 |
| 18 |
| 35 |
| 12 |
| 35 |
| 1 |
| 35 |
| 9 |
| 7 |


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
| 3 |
| 2 |
| ||
| 2 |
| OM |
| ON |
查看答案和解析>>
科目:高中数学 来源: 题型:
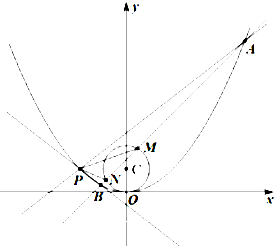 设点P(-2,1)在抛物线x2=2py(p>0)上,且到圆C:x2+(y+b)2=1上点的最小距离为1.
设点P(-2,1)在抛物线x2=2py(p>0)上,且到圆C:x2+(y+b)2=1上点的最小距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 2 |
| x2 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| p |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
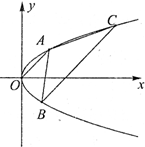 已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.
已知点A,B,C是抛物线L:y2=2px(p>0)上的不同的三点,O为坐标原点,直线OA∥BC,且抛物线L的准线方程为x=-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com