
设函数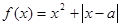 (
(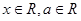 ).
).
(1)讨论 的奇偶性;
的奇偶性;
(2)当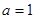 时,求
时,求 的单调区间;
的单调区间;
(3)若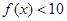 对
对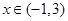 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)当a=0时,f(x)为偶函数;当a≠0时,f(x)为非奇非偶函数;
(2)(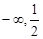 )为减区间,[
)为减区间,[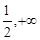 )为增区间;(3)
)为增区间;(3)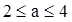
解析试题分析:(1)当a=0时,f(x)为偶函数;当a≠0时,f(x)为非奇非偶函数;
(2)a=1时,f(x)=x2+|x-1|=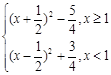 ,再进行配方,利用函数的图象,确定函数的单调区间;(3)f(x)=x2+|x-a|<10对x∈(-1,3)恒成立,等价于x2-10<x-a<10-x2,分离参数可得
,再进行配方,利用函数的图象,确定函数的单调区间;(3)f(x)=x2+|x-a|<10对x∈(-1,3)恒成立,等价于x2-10<x-a<10-x2,分离参数可得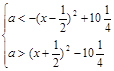 ,对x∈(-1,3)恒成立,从而可求实数a的取值范围.
,对x∈(-1,3)恒成立,从而可求实数a的取值范围.
试题解析:(1)若a=0时,f(x)为偶函数,若a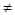 0时,f(x)为非奇非偶函数 3分
0时,f(x)为非奇非偶函数 3分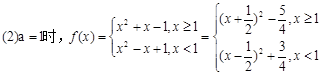
得f(x):(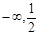 )为减区间,[
)为减区间,[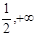 )为增区间 7分
)为增区间 7分
(3)f(x)=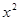 +|x-a|<10对
+|x-a|<10对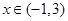 恒成立,
恒成立,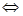
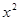 -10<x-a<10 -
-10<x-a<10 -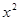
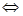
 14分
14分
考点:1.函数的单调性及单调区间;2.函数奇偶性的判断;3.函数恒成立问题


科目:高中数学 来源: 题型:解答题
已知函数f(x)是定义在[-3,3]上的奇函数,且当x∈[0,3]时,f(x)=x|x-2|
⑴在平面直角坐标系中,画出函数f(x)的图象
⑵根据图象,写出f(x)的单调增区间,同时写出函数的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com