
【题目】经市场调查,某商品在过去的20天内的价格![]() (单位:元)与销售量
(单位:元)与销售量![]() (单位:件)均为时间
(单位:件)均为时间![]() (单位:天)的函数,且价格满足
(单位:天)的函数,且价格满足![]() ,销售量满足
,销售量满足![]() ,其中
,其中![]() ,
, ![]() .
.
(1)请写出该商品的日销售额![]() (单位:元)与时间
(单位:元)与时间![]() (单位:天)的函数解析式;
(单位:天)的函数解析式;
(2)求该商品的日销售额的最小值.
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() ,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以O为极点,x轴非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρsin2θ=4cosθ,直线![]() 的参数方程为:
的参数方程为: 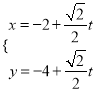 (t为参数),两曲线相交于M,N两点.
(t为参数),两曲线相交于M,N两点.
(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;
(Ⅱ)若P(﹣2,﹣4),求|PM|+|PN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某班的一次期末考试中,随机的抽取了七位同学的数学(满分150分)、物理(满分110分)成绩如下表所示,数学、物理成绩分别用特征量![]() 表示,
表示,
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求![]() 关于t的回归方程;
关于t的回归方程;
(2)利用(1)中的回归方程,分析数学成绩的变化对物理成绩的影响,并估计该班某学生数学成绩130分时,他的物理成绩(精确到个位).
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
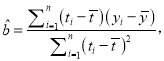
![]() .
. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最大值4 和最小值1,设
上有最大值4 和最小值1,设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在区间
在区间![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com