
科目:高中数学 来源:2017届江苏扬州中学等七校高三上期中联考数学试卷(解析版) 题型:解答题
对于两个定义域均为D的函数f(x),g(x),若存在最小正实数M,使得对于任意x∈D,都有|f(x)-g(x)|≤M,则称M为函数f(x),g(x)的“差距”,并记作||f(x),g(x)||.
(1)求f(x)=sinx(x∈R),g(x)=cosx(x∈R)的差距;
(2)设f(x)= (x∈[1,
(x∈[1,  ]),g(x)=mlnx (x∈[1,
]),g(x)=mlnx (x∈[1,  ]).(e≈2.718)
]).(e≈2.718)
①若m=2,且||f(x),g(x)||=1,求满足条件的最大正整数a;
②若a=2,且||f(x),g(x)||=2,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届江苏扬州中学等七校高三上期中联考数学试卷(解析版) 题型:填空题
在△ABC的边AB上随机取一点P,记△CAP和△CBP的面积分别为S1和S2,则 的概率是 .
的概率是 .
查看答案和解析>>
科目:高中数学 来源:2017届贵州遵义市高三上期中数学(文)试卷(解析版) 题型:解答题
如图,四边形 是边长为2的菱形,
是边长为2的菱形,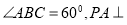 平面
平面 ,
,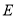 为
为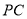 的中点.
的中点.
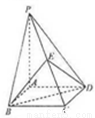
(1)求证:平面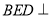 平面
平面 ;
;
(2)若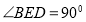 ,求三棱锥
,求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2017届贵州遵义市高三上期中数学(理)试卷(解析版) 题型:选择题
某企业为节能减排,用9万元购进一台新设备用于生产,第一年需运营费用2万元,从第二年起,每年运营费用均比上一年增加3万元,该设备每年生产的收入均为21万元,设该设备使用了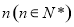 年后,盈利总额达到最大值(盈利额等于收入减去成本),则
年后,盈利总额达到最大值(盈利额等于收入减去成本),则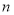 等于( )
等于( )
A.6 B.7 C.8 D.7或8
查看答案和解析>>
科目:高中数学 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
已知平面直角坐标系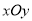 中,圆
中,圆 的参数方程为
的参数方程为 (
(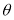 为参数,
为参数, ).以直角坐标系原点
).以直角坐标系原点 为极点,
为极点,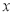 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线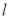 的极坐标方程为
的极坐标方程为 .
.
(1)求圆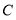 的圆心的极坐标;
的圆心的极坐标;
(2)当圆 与直线
与直线 有公共点时,求
有公共点时,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com