练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某工厂生产A、B两种产品，已知制造A产品1kg要用煤9t，电力4kw，劳力（按工作日计算）3个；制造B产品1kg要用煤4t，电力5kw，劳力10个．又已知制成A产品1kg可获利7万元，制成B产品1kg可获利12万元．现在此工厂由于受到条件限制只有煤360t，电力200kw，劳力300个，在这种条件下应生产A、B产品各多少kg能获得最大的经济效益？
    分析：设出变量，确定不等式组，可得可行域，利用线性规划知识，可求最值．
    解答：解：设工厂应生产A产品xkg，B产品ykg，利润z万元，则由题意得
    9x+4y≤360
    4x+5y≤200
    3x+10y≤300
    x≥0，y≥0

    利润函数为z=7x+12y
    作出不等式组表示的平面区域
    由z=7x+12y，变为y=-
    7
    12
    x+
    z
    12
    ，可知直线经过M点时，z取得最大值
    由
    3x+10y=300
    4x+5y=200
    ，可得x=20，y=24，∴M（20，24）
    ∴zmax=7×20+12×24=428
    答：工厂应生产A产品20kg，B产品24kg，利润最大为428万元．
    点评：本题考查线性规划知识的运用，考查学生的计算能力，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某工厂生产A．B两种不同成本的产品，由于市场变化，A产品连续两次提价20%，同时B产品连续两次降价20%，结果都以23.04元售出．若同时出售A．B产品各一件，试问厂家是亏还是赚，亏赚多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

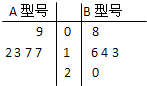    精英家教网某工厂生产A、B两种型号的产品，每种型号的产品在出厂时按质量分为一等品和二等品．为便于掌握生产状况，质检时将产品分为每20件一组，分别记录每组一等品的件数．现随机抽取了5组的质检记录，其一等品数茎叶图如图所示：
    （1）试根据茎叶图所提供的数据，分别计算A、B两种产品为一等品的概率PA、PB；
    （2）已知每件产品的利润如表一所示，用ξ、η分别表示一件A、B型产品的利润，在（1）的条件下，求ξ、η的分布列及数学期望（均值）Eξ、Eη；
    （3）已知生产一件产品所需用的配件数和成本资金如表二所示，该厂有配件30件，可用资金40万元，设x、y分别表示生产A、B两种产品的数量，在（2）的条件下，求x、y为何值时，z=xEξ+yEη最大？最大值是多少？（解答时须给出图示）
    表一
    等级
    利润
    产品    		 一等品 二等品
    A型 4（万元） 3（万元）
    B型 3（万元） 2（万元）
    表二
    项目
    用量
    产品    		 配件（件） 资金（万元）
    A型 6 4
    B型 2 8

    查看答案和解析>>

    科目：高中数学 来源：2011年安徽省淮安五校高一上学期期末考试数学试卷 题型：填空题

    某工厂生产A、B两种成本不同的产品，由于市场变化，A产品连续两次提价20%，同时B产品连续两次降20%，结果都以每件23.04元售出，若同时出售A、B产品各一件，则_____________(填盈或亏) _________元。

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年江苏省淮安市高一上学期期末考试数学试卷 题型：填空题

    某工厂生产A、B两种成本不同的产品，由于市场变化，A产品连续两次提价20%，同时B产品连续两次降20%，结果都以每件23.04元售出，若同时出售A、B产品各一件，则_____________(填盈或亏) _________元。

     

    查看答案和解析>>

    同步练习册答案