
 ,其中
,其中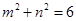 ,则该三棱锥体积的最大值为
,则该三棱锥体积的最大值为A. | B. | C. | D. |
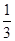 ×
× abc=
abc=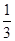 abc. a2+b2=2,b2+c2=n2,a2+c2=m2,所以2(a2+b2+c2)=n2+m2+2=8. a2+b2+c2=4.因为4≥3
abc. a2+b2=2,b2+c2=n2,a2+c2=m2,所以2(a2+b2+c2)=n2+m2+2=8. a2+b2+c2=4.因为4≥3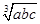
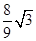 此时a=b=c,与n2+m2=6,a2+b2=2,矛盾,所以选项B不正确;则C不正确;当底面三角形是等腰三角形时,m=n=
此时a=b=c,与n2+m2=6,a2+b2=2,矛盾,所以选项B不正确;则C不正确;当底面三角形是等腰三角形时,m=n=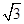
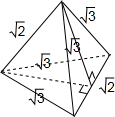
 ,选D.
,选D.

科目:高中数学 来源:不详 题型:单选题
 ,求其直径
,求其直径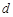 的一个近似公式
的一个近似公式 . 人们还用过一些类似的近似公式. 根据
. 人们还用过一些类似的近似公式. 根据 判断,下列近似公式中最精确的一个是( )
判断,下列近似公式中最精确的一个是( )A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,则球的表面积( )
,则球的表面积( ) B、
B、 C、
C、 D、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com