
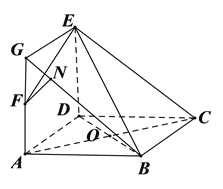
【题目】如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列说法中正确的个数( )

①AC∥平面BEF;
②B、C、E、F四点可能共面;
③若EF⊥CF,则平面ADEF⊥平面ABCD;
④平面BCE与平面BEF可能垂直
A.0B.1C.2D.3
【答案】C
【解析】
根据折叠前后线段、角的变化情况,由线面平行、面面垂直的判定定理和性质定理对各命题进行判断,即可得出答案.
对①,在图②中,连接![]() 交于点
交于点![]() ,取
,取![]() 中点,连接MO,易证AOMF为平行四边形,即AC//FM,所以AC//平面BEF,故①正确;
中点,连接MO,易证AOMF为平行四边形,即AC//FM,所以AC//平面BEF,故①正确;
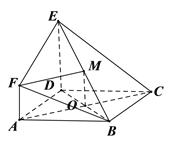
对②,如果B、C、E、F四点共面,则由BC//平面ADEF,可得BC//EF,又AD//BC,所以AD//EF,这样四边形ADEF为平行四边形,与已知矛盾,故②不正确;
对③,在梯形ADEF中,由平面几何知识易得EF![]() FD,又EF
FD,又EF![]() CF,∴EF
CF,∴EF![]() 平面CDF,
平面CDF,
即有CD![]() EF,∴CD
EF,∴CD![]() 平面ADEF,则平面ADEF
平面ADEF,则平面ADEF![]() 平面ABCD,故③正确;
平面ABCD,故③正确;
对④,在图②中,延长AF至G,使得AF=FG,连接BG,EG,易得平面BCE![]() 平面ABF,BCEG四点共面.过F作FN
平面ABF,BCEG四点共面.过F作FN![]() BG于N,则FN
BG于N,则FN![]() 平面BCE,若平面BCE
平面BCE,若平面BCE![]() 平面BEF,
平面BEF,
则过F作直线与平面BCE垂直,其垂足在BE上,矛盾,故④错误.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产![]() 万件,需另投入流动成本
万件,需另投入流动成本![]() 万元,当年产量小于
万元,当年产量小于![]() 万件时,
万件时,![]() (万元);当年产量不小于7万件时,
(万元);当年产量不小于7万件时,![]() (万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(1)写出年利润![]() (万年)关于年产量
(万年)关于年产量![]() (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程是 (φ为参数,a>0),直线l的参数方程是
(φ为参数,a>0),直线l的参数方程是![]() (t为参数),曲线C与直线l有一个公共点在x轴上,以坐标原点为极点,x轴的正半轴为极轴建立坐标系.
(t为参数),曲线C与直线l有一个公共点在x轴上,以坐标原点为极点,x轴的正半轴为极轴建立坐标系.
(1)求曲线C的普通方程;
(2)若点A(ρ1,θ),B(ρ2,θ+![]() ),C(ρ3,θ+
),C(ρ3,θ+![]() )在曲线C上,求
)在曲线C上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
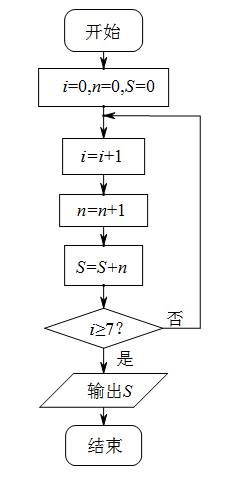
A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
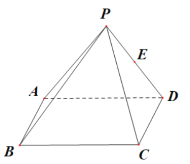
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,侧面
,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)在棱![]() 上取一点
上取一点![]() 使直线
使直线![]() ∥平面
∥平面![]() 并证明;
并证明;
(2)在(1)的条件下,当棱![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与底面
与底面![]() 所成角为
所成角为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com