
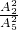 +
+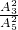 =
= ;
;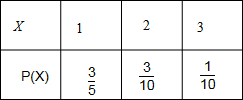
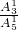 =
= ,P(X=2)=
,P(X=2)=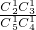 =
= ,P(X=3)=
,P(X=3)=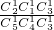 =
= ,∴其分布列如下表:
,∴其分布列如下表: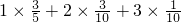 =
= .
.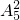 种,从1、3、5三个数中依次取两个数有
种,从1、3、5三个数中依次取两个数有 种,从2、4两个数中依次取两个数有
种,从2、4两个数中依次取两个数有 ,进而根据互斥事件的概率计算公式即可得出;
,进而根据互斥事件的概率计算公式即可得出; 种方法,而从给出的5个球中任意摸出一个球可有
种方法,而从给出的5个球中任意摸出一个球可有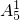 种方法,根据概率的计算公式即可求出P(X=1),同理即可计算出P(X=2),P(X=3),即可得出其分布列.再利用相互独立事件的概率、数学期望的公式即可得出.
种方法,根据概率的计算公式即可求出P(X=1),同理即可计算出P(X=2),P(X=3),即可得出其分布列.再利用相互独立事件的概率、数学期望的公式即可得出.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高三第三次模拟考试数学(文) 题型:解答题
(本小题满分12分)
在一个盒子中放有标号分别为1、2、3的三张卡片,现从这个盒子中有放回地先后抽取两张卡片,并记它们的标号分别为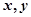 ,设
,设 ,
,
(1)求事件“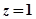 ”发生的概率;
”发生的概率;
(2)求 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率。
取得最大值”的概率。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省哈尔滨九中高考数学三模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省哈九中高三第三次模拟考试数学(文) 题型:解答题
(本小题满分12分)
在一个盒子中放有标号分别为1、2、3的三张卡片,现从这个盒子中有放回地先后抽取两张卡片,并记它们的标号分别为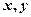 ,设
,设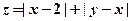 ,
,
(1)求事件“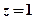 ”发生的概
”发生的概 率;
率;
(2)求 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率。
取得最大值”的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com