
【题目】已知![]() 为常数,函数
为常数,函数![]() .
.
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,对于给定的
时,对于给定的![]() ,且
,且![]() ,
,![]() ,证明:关于
,证明:关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有一个实根.
内有一个实根.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣mx(m∈R).
﹣mx(m∈R).
(1)当m=0时,求函数f(x)的零点个数;
(2)当m≥0时,求证:函数f(x)有且只有一个极值点;
(3)当b>a>0时,总有 ![]() >1成立,求实数m的取值范围.
>1成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试无纸化阅卷的评分规则的程序如图所示,x1 , x2 , x3为三个评卷人对同一道题的独立评分,p为该题的最终得分,当x1=6,x2=9,p=8.5时,x3=( ) 
A.11
B.10
C.8
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x).对任意的a,b∈R.满足:f(a+b)=f(a)f(b),当x>0时,有f(x)>1,其中f(1)=2.
(1)求f(0),f(﹣1)的值;
(2)判断该函数的单调性,并证明;
(3)求不等式f(x+1)<4的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意x,y∈R,都有f(x+y)=f(x)+f(y),且x>0时,f(x)<0, f(1)=-2.
(1)求证:f(x)是奇函数;
(2)判断函数![]() 的单调性
的单调性
(3)求f(x)在[-3,3]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() ,满足
,满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”,![]() 是它的均值点.
是它的均值点.
(1)![]() 是否是
是否是![]() 上的“平均值函数”,如果是请找出它的均值点;如果不是,请说明理由;
上的“平均值函数”,如果是请找出它的均值点;如果不是,请说明理由;
(2)现有函数![]() 是
是![]() 上的平均值函数,则求实数
上的平均值函数,则求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图程序框图的算法思路源于我国古代数学名著《九章算术》中的某一种算法.执行该程序框图,输入分别为98,63,则输出的结果是( ) 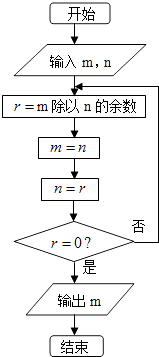
A.14
B.18
C.9
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com