
闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧綊鏌熼梻瀵割槮缁炬儳缍婇弻鐔兼⒒鐎靛壊妲紒鐐劤缂嶅﹪寮婚悢鍏尖拻閻庨潧澹婂Σ顔剧磼閻愵剙鍔ょ紓宥咃躬瀵鎮㈤崗灏栨嫽闁诲酣娼ф竟濠偽i鍓х<闁绘劦鍓欓崝銈囩磽瀹ュ拑韬€殿喖顭烽幃銏ゅ礂鐏忔牗瀚介梺璇查叄濞佳勭珶婵犲伣锝夘敊閸撗咃紲闂佺粯鍔﹂崜娆撳礉閵堝棛绡€闁逞屽墴閺屽棗顓奸崨顖氬Е婵$偑鍊栫敮鎺楀磹瑜版帒鍚归柍褜鍓熼弻锝嗘償閵忕姴姣堥梺鍛婄懃閸燁偊鎮惧畡鎵殾闁搞儜灞绢棥闂佽鍑界徊濠氬礉鐎n€兾旈崨顔规嫼闂侀潻瀵岄崢濂稿礉鐎n喗鐓曢柕濞垮劤缁夎櫣鈧娲橀崝娆撳箖濞嗗浚鍟呮い鏃囨閻︽粓姊绘笟鈧ḿ褔鎮ч崱妞㈡稑螖閸愵亞鐣堕梺绋挎湰缁海澹曟總鍛婄厓鐟滄粓宕滃杈╃當闁绘梻鍘ч悞鍨亜閹哄棗浜鹃梺浼欑到閸㈡煡銈导鏉戦唶妞ゆ劧绲惧▍宥夋⒒娴h櫣甯涢柛銊╂涧铻炴繛鍡樺灍閸嬫捇妫冨☉姘卞姱濠殿喖锕ュ钘壩涢崘銊㈡婵﹩鍓﹂弳顐g節绾版ɑ顫婇柛瀣嚇閵嗗啴宕卞☉妯肩杽闂侀潧饪撮悡鍫澪i崜褏纾藉ù锝勭矙閸濇椽鎮介銈囩瘈妤犵偛鍟撮崺锟犲川椤撶媭妲伴梻浣藉亹閳峰牓宕楀☉姘潟婵犻潧顑嗛埛鎺懨归敐鍫燁仩閻㈩垱绋戦妴鎺戭潩椤撗勭杹閻庤娲樻繛濠囧极閹版澘骞㈡俊顖氭惈娴煎酣姊绘笟鈧埀顒傚仜閼活垱鏅堕幘顔界厸閻忕偟鍋撶粈瀣偓瑙勬礈閸樠囧煘閹达箑鐐婇柤鍝ヮ暜妤犲繘姊婚崒娆戭槮闁圭寽銈嗘噷闂備礁婀遍幊鎾趁洪鐑嗗殨濠电姵鑹鹃悞娲煕閹扳晛濡跨紒鎰仱閺岋綀绠涢弴鐐版勃闂佹悶鍔嶇换鍌炲煝娴犲鏁傞柛娑卞灣閻﹀牓姊洪棃娑氱疄闁搞劍妞藉畷鐢稿焵椤掆偓閳规垿鍩ラ崱妞剧凹缂備浇顕ч崐鍧楀箖閹呮殝闁逛絻娅曢弬鈧梻浣虹《濡狙囧疾濞戙垹绠栭柟杈鹃檮閳锋垹绱掗娑欑濠⒀勭叀閺屾盯寮埀顒傛暜閻愮儤鍤嶉弶鍫涘妿缁♀偓濠殿喗锕╅崢鎼佸箯濞差亝鈷戦柛娑橈功缁犳捇鎮楀鐓庡⒋闁糕斁鍋撳銈嗗笂閻掞箓宕愰幇鐗堢厵妞ゆ梻鐓鍫濈厴闁瑰濮崑鎾绘晲閸涱垯绮甸梺鍝勬噺缁矂鈥旈崘顔嘉ч柛鈩冾殔椤洭姊虹粙鍖℃敾妞ゃ劌鐗婄粩鐔煎即閻旀椽妾紓浣割儓濞夋洘顨ラ崶顒佲拺闁告挻褰冩禍婵堢磼鐎n偄鐏﹀ǎ鍥э躬閹墽浠︾粙澶稿闁荤喐鐟ョ€氼厾绮堥埀顒勬⒑濞茶澧柕鍫熸倐瀹曟椽鍩€椤掍降浜滈柟鐑樺灥閺嬨倖绻涢崗鐓庡缂佺粯鐩畷锝嗗緞閸涱垳绐楅梻浣芥〃缁讹繝宕抽敐澶屽祦闁圭儤鍤﹂弮鍌楀亾閿濆骸澧伴柍绗哄€栫换婵嬫偨闂堟稈鏋呭┑鐐板尃閸ヨ埖鏅為梺鍦濠㈡﹢寮告笟鈧弻娑㈠即閵娿儳浠梺缁樻尪閸ㄧ儤绌辨繝鍥舵晬婵炲棙甯╅崝鍛攽閳╁啫绲婚柛銏$叀閳ワ妇鎹勯妸锕€鏋傞梺鍛婃处閸撴盯藝閺夊簱鏀芥い鏃傘€嬮弨缁樹繆閻愯埖顥夐柣锝囧厴婵℃悂鏁傞崜褏妲囬梻浣告啞濞诧箓宕㈤崜褏鐜绘俊銈呮噺閳锋帒霉閿濆懏鍤堥柛锔诲幐閸嬫挸鈽夐幒鎾寸彆缂備胶绮粙鎺旀崲濠靛鐐婄憸蹇涙偩妤e啯鐓熼煫鍥ㄦ礀娴犫晝鎮▎鎾寸厸閻庯綆浜崣鍕煛瀹€鈧崰鏍嵁閸℃凹妾ㄩ梺鎼炲€楅崰鏍蓟濞戞﹩娼ㄩ柍褜鍓氱粋宥囨崉娓氼垱缍庡┑鐐叉▕娴滄粍瀵奸悩缁樼厱闁哄洢鍔屾晶顕€鏌涚€n亞效婵﹥妞藉畷銊︾節閸愵亜寮抽梻浣规た閸樺ジ宕愰崸妤冨祦闁告劦鐓堝ḿ銊╂煃瑜滈崜鐔肩嵁閸愵喖鐓涢柛娑卞枛娴犳椽姊哄Ч鍥х伄妞わ綆鍠氬Σ鎰板蓟閵夛腹鎷绘繛杈剧秬濞咃絿鏁☉銏$厽闁绘梹娼欓悘鑼偓瑙勬礃閸ㄥ潡鐛Ο鑲╃<婵☆垳鍘ч獮鍫ユ⒒娓氣偓濞佳勭仚闂佺ǹ瀛╂繛濠傜暦濞差亝鏅查柛銉到娴滅偓绻涢崼婵堜虎闁哄绋掗妵鍕敇閵忊剝鏆犳繛锝呮搐閿曨亪鐛弽銊﹀闁告縿鍎遍獮鎰版⒒娴e懙褰掑嫉椤掑嫭鍎楁い鏃€宕樻慨鍐裁归悩宸剱闁抽攱甯掗湁闁挎繂鎳忛崵鍫㈡喐閻楀牆绗掗悗姘槹閵囧嫰骞掗幋婵冨亾婵犳碍鍎楁繛鍡樻尰閻撴瑩寮堕崼鐔峰姢闁伙附绮撻弻鈩冩媴缁嬪簱鍋撻崸妤€钃熼柕濞炬櫆閸嬪棝鏌涚仦鍓р槈妞ゅ骏鎷�濠电姷鏁告慨鐑藉极閸涘﹥鍙忛柣鎴f閺嬩線鏌涘☉姗堟敾闁告瑥绻橀弻锝夊箣閿濆棭妫勯梺鍝勵儎缁舵岸寮诲☉妯锋婵鐗婇弫楣冩⒑閸涘﹦鎳冪紒缁橈耿瀵鏁愭径濠勵吅闂佹寧绻傚Λ顓炍涢崟顖涒拺闁告繂瀚烽崕搴g磼閼搁潧鍝虹€殿喛顕ч埥澶娢熼柨瀣垫綌婵犳鍠楅〃鍛存偋婵犲洤鏋佸Δ锝呭暞閳锋垿鏌涘☉姗堝姛闁瑰啿鍟扮槐鎺旂磼濮楀牐鈧法鈧鍠栭…鐑藉极閹邦厼绶炲┑鐘插閸氬懘姊绘担鐟邦嚋缂佽鍊歌灋妞ゆ挾鍊e☉銏犵妞ゆ牗绋堥幏娲⒑閸涘﹦绠撻悗姘卞厴瀹曟洘鎯旈敐鍥╋紲闂佸吋鎮傚ḿ褔宕搹鍏夊亾濞堝灝鏋涙い顓犲厴楠炲啴濮€閵堝懐顦ч柣蹇撶箲閻楁鈧矮绮欏铏规嫚閺屻儱寮板┑鐐板尃閸曨厾褰炬繝鐢靛Т娴硷綁鏁愭径妯绘櫓闂佸憡鎸嗛崪鍐簥闂傚倷娴囬鏍垂鎼淬劌绀冮柨婵嗘閻﹁京绱撻崒姘偓椋庢閿熺姴闂い鏇楀亾鐎规洖缍婇獮搴ㄦ寠婢跺矈鍞归梻渚€娼х换鎺撴叏椤撶倣锝夊醇閵夛妇鍘棅顐㈡处濞叉牕鏆╂俊鐐€栭幐璇差渻閽樺娼栨繛宸簻娴肩娀鏌涢弴銊ヤ簼婵炲牊绮撳铏圭矙濞嗘儳鍓遍梺鍦嚀濞差厼顕g拠娴嬫闁靛繒濮堣閺屾稑鈽夐崡鐐碘偓铏规喐閺冨牆钃熼柨娑樺濞岊亪鏌涢幘妤€瀚崹鍗炩攽閻樻鏆滅紒杈ㄦ礋瀹曟顫滈埀顒勫Υ娴g硶鏋庨柟鐐綑娴滄鏌熼悡搴f憼閽冮亶鎮楀顐ょ煓婵﹤顭峰畷鎺戔枎閹邦喓鍋樻繝纰樺墲閵囨粓宕濇惔锝呭灊闁割偆鍠愭刊鎾偣閸ャ儱鍔滄俊鐐扮矙閵嗕礁顫滈埀顒佹叏閳ь剟鏌eΟ鐓庡妺闁硅弓鍗冲缁樻媴閸涘﹥鍎撳┑鐐存綑鐎氼喖危閹版澘鍗抽柕蹇娾偓鍏呯棯闂備線鈧偛鑻晶瀛樻叏婵犲啯銇濈€规洦鍋婂畷鐔碱敆閳ь剛绮e☉銏♀拺缂佸绨遍惇瀣煕鐎n亷鏀诲ǎ鍥э躬閹粓鎳為妷锔界彆闂佸搫顦遍崑鐐寸珶閸℃稒鍎庨幖娣妽閳锋帒霉閿濆洦鍤€妞ゆ洘绮嶆穱濠囶敃閿涘嫮鐛㈠銈冨灪娣囨椽藝閺屻儲鐓冮悹鍥皺瀛濆銈嗘尭閸氬顕ラ崟顓涘亾閿濆骸澧鐐茬У娣囧﹪鎮欓鍕ㄥ亾閺嵮屾綎濠电姵纰嶉崑銈夋煛閸屾氨姘ㄩ柡瀣⒐缁绘繃绻濋崒娑樻珴闂佺ǹ顑嗛幐楣冨箟閹绢喖绀嬫い鎺戝亞濡茬増淇婇悙顏勨偓鎴﹀礉鐏炶娇娑樜旈崪浣规櫔闂侀潧顦弲娑氱矆鐎n偁浜滈柟鐑樺灥閳ь剙顭烽幆渚€宕奸悢铏诡啎闁哄鐗嗘晶浠嬪礆閺夋鐔嗛柣鐔峰簻瀹搞儵鎽堕悙瀵哥瘈濠电姴鍊绘晶娑㈡煃闁垮娴柡灞剧〒娴狅箓骞戦幇顒夋闂備線鈧偛鑻晶瀛樸亜閵夛附灏甸柛鎺撳浮瀹曞ジ鎮㈤搹瑙勫殞闂備線鈧偛鑻晶鎾煟濞戝崬鏋熺€垫澘瀚伴獮鍥敆閸屾瑧绀堥梻浣哄劦閸撴繄鏁繝鍥ㄥ€块柨鏇楀亾妞ゎ亜鍟粋鎺斺偓锝庝簼閻庮剟姊洪崨濠傚Е闁哥姵鐗滄竟鏇㈠礂閸忕厧寮垮┑鈽嗗灥椤曆囧极閸撗呯<闁告鍋涢懜褰掓煃鐟欏嫬鐏撮柟顔规櫊椤㈡瑩鎳栭埡鈧槐姗€姊绘担铏广€婇柡鍛矒閹囨偐閼碱剚娈惧┑鐘绘涧椤戝懘宕¢幎鑺ョ厪闊洦娲栧瓭閻庢鍠氶崗妯侯潖濞差亝顥堟繛鎴i哺瀛濋梻浣告惈閹冲繒鍒掗幘璇茬畺闁跨喓濮甸崑鍕煕韫囨艾浜归柛妯兼暬濮婄粯绗熼崶褍浼庣紓浣哄У閸ㄥ灝顕g粙搴撴闁靛骏绱曢崢閬嶆⒑閸濆嫬鈧綊顢栧▎鎾崇?闁哄啫鐗婇悡娑㈡倶閻愬灚娅曢弫鍫ユ⒑閸濆嫯顫﹂柛鏂块叄閸┾偓妞ゆ帒锕︾粔闈浢瑰⿰鍛沪閻庣數鍘ч悾婵嬪礋椤戣姤瀚奸梺鑽ゅТ濞茬娀鍩€椤掑啯鐝柣蹇撶墢缁辨捇宕掑姣欍垽鏌ㄩ弴銊ら偗闁诡喕鍗抽、娆撴偩瀹€鈧幊婵嬫⒑闁偛鑻晶鎾煟濞戝崬娅嶆鐐村笒铻栭柍褜鍓涚划濠氭晲閸℃瑧鐦堥梺鍓茬厛閸嬪嫭鎱ㄦ径鎰厓鐟滄粓宕滃┑鍡忔瀺闁哄洨濮靛畷鍙夌節闂堟侗鍎愰柛瀣ㄥ姂濮婂宕奸悢琛℃)缂備緡鍠栭悥鐓庮潖濞差亝鍋¢柡澶嬪濮f劗绱撴担铏瑰笡闁挎岸鏌i敐鍛Щ闁宠鍨垮畷杈疀閺冨倵鍋撴繝姘拺閻熸瑥瀚崝銈夋煟閵堝懏鍠樻鐐搭殜瀵挳濮€閳锯偓閹疯櫣绱撻崒娆戝妽閽冮亶鏌嶉柨瀣诞闁哄本绋戣灒闁绘ê寮堕崳浠嬫煟椤撶偞顥㈤柡灞剧洴瀵挳濡搁妷褌鐢婚梻浣虹帛閹稿摜鎹㈠鈧璇测槈閵忊晜鏅濋梺鎸庣箓濞层劑鎮鹃崫鍕垫富闁靛牆鍟崝婊呯磼椤旇偐效濠碉紕鏁诲畷鐔碱敊閸撗勬緫闂備線娼ч¨鈧紒鐘冲灴椤㈡棃鏁撻敓锟�
 (文科)侧棱长为3
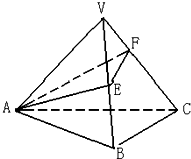
(文科)侧棱长为3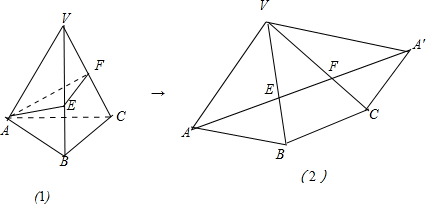 解:如图所示:沿着侧棱VA把正三棱锥V-ABC展开在一个平面内,如图(2),
解:如图所示:沿着侧棱VA把正三棱锥V-ABC展开在一个平面内,如图(2),



