
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以平面直角坐标系的原点为极点,
),以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 被圆截得的弦长为
被圆截得的弦长为![]() 时,求
时,求![]() 的值.
的值.
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若
为参数),若![]() ,垂足为
,垂足为![]() ,求
,求![]() 点的极坐标.
点的极坐标.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线x2=4y的焦点F和点A(-1,8),点P为抛物线上一点,则|PA|+|PF|的最小值为( )
A. 16 B. 6 C. 12 D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
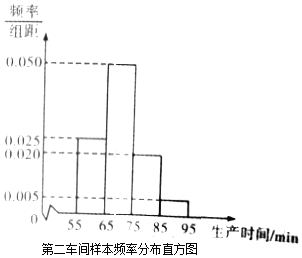
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中,随机抽取3人,记抽取的生产时间小于65min的工人人数为随机变量X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ②函数
②函数![]() 有3个零点
有3个零点
③![]() 的解集为
的解集为![]() ④
④![]() ,都有
,都有![]()
其中正确命题的个数是( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们要计算由抛物线![]() ,x轴以及直线
,x轴以及直线![]() 所围成的区域的面积S,可用x轴上的分点
所围成的区域的面积S,可用x轴上的分点![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、1将区间
、1将区间![]() 分成n个小区间,在每个小区间上做一个小矩形,使矩形的左端点在抛物线
分成n个小区间,在每个小区间上做一个小矩形,使矩形的左端点在抛物线![]() 上,这些矩形的高分别为
上,这些矩形的高分别为![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,矩形的底边长都是
,矩形的底边长都是![]() ,设所有这些矩形面积的总和为
,设所有这些矩形面积的总和为![]() ,为求S,只须令分割的份数n无限增大,
,为求S,只须令分割的份数n无限增大,![]() 就无限趋近于S,即
就无限趋近于S,即![]() .
.
(1)求数列![]() 的通项公式,并求出S;
的通项公式,并求出S;
(2)利用相同的思想方法,探求由函数![]()
![]() 的图象,x轴以及直线
的图象,x轴以及直线![]() 和
和![]() 所围成的区域的面积T.
所围成的区域的面积T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O经过椭圆C:![]() =1(a>b>0)的两个焦点以及两个顶点,且点(b,
=1(a>b>0)的两个焦点以及两个顶点,且点(b,![]() )在椭圆C上.
)在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与圆O相切,与椭圆C交于M、N两点,且|MN|=![]() ,求直线l的倾斜角.
,求直线l的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】边长为![]() 的等边三角形内任一点到三边距离之和为定值,这个定值等于
的等边三角形内任一点到三边距离之和为定值,这个定值等于![]() ;将这个结论推广到空间是:棱长为
;将这个结论推广到空间是:棱长为![]() 的正四面体内任一点到各面距离之和等于________________.(具体数值)
的正四面体内任一点到各面距离之和等于________________.(具体数值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com