
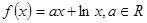
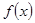 的极值;
的极值;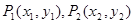 ,如果存在曲线上的点
,如果存在曲线上的点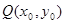 ,且
,且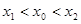 ,使得曲线在点
,使得曲线在点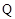 处的切线
处的切线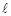 ∥
∥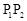 ,则称
,则称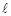 为弦
为弦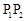 的伴随切线。特别地,当
的伴随切线。特别地,当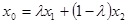 ,
,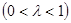 时,又称
时,又称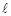 为
为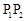 的λ——伴随切线。
的λ——伴随切线。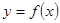 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;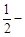 伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。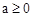 时,
时,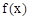 没有极值;
没有极值;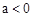 时,
时,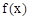 的极大值为
的极大值为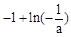 ,没有极小值。(Ⅱ)见解析
,没有极小值。(Ⅱ)见解析 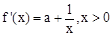
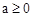 ,
,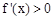 ,函数
,函数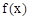 在
在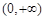 内是增函数,
内是增函数,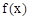 没有极值。 当
没有极值。 当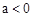 时,令
时,令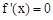 ,得
,得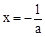 。
。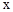 变化时,
变化时,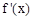 与
与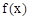 变化情况如下表:
变化情况如下表: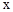 | 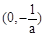 | 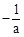 | 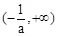 |
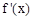 | + | 0 | - |
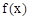 | 单调递增 | 极大值 | 单调递减 |
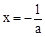 时,
时,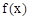 取得极大值
取得极大值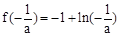 。
。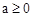 时,
时,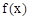 没有极值;
没有极值;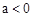 时,
时,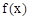 的极大值为
的极大值为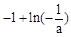 ,没有极小值。
,没有极小值。 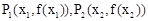 是曲线
是曲线 上的任意两点,要证明
上的任意两点,要证明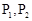 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点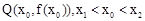 ,使得
,使得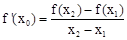 ,且点
,且点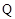 不在
不在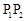 上。
上。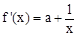 ,即证存在
,即证存在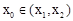 ,使得
,使得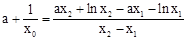 ,即
,即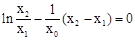 成立,且点
成立,且点 不在
不在 上。 …………………8分
上。 …………………8分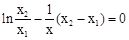 在
在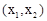 内有解。…
内有解。…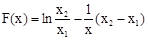 ,则
,则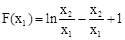 。
。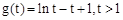 ,
, ,
,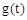 在
在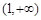 内是减函数,∴
内是减函数,∴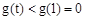 。
。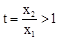 ,则
,则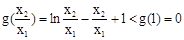 ,即
,即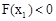 。……9分
。……9分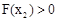 。∴
。∴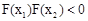 。
。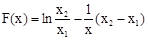 在
在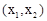 内有零点。
内有零点。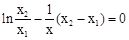 在
在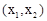 内有解
内有解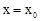 。又对于函数
。又对于函数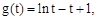 取
取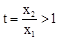 ,则
,则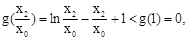
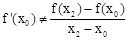 ,即点Q不在
,即点Q不在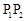 上。
上。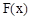 是增函数,∴
是增函数,∴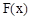 的零点是唯一的,
的零点是唯一的, 在
在 内有唯一解。
内有唯一解。 上任意一条弦均有伴随切线,并且伴随切线是唯一的。
上任意一条弦均有伴随切线,并且伴随切线是唯一的。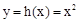 ,则曲线
,则曲线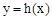 的任意一条弦均有
的任意一条弦均有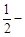 伴随切线。
伴随切线。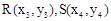 是曲线C上任意两点
是曲线C上任意两点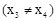 ,
,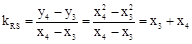 ,
,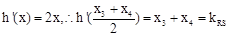 ,
, 的任意一条弦均有
的任意一条弦均有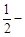 伴随切线。
伴随切线。 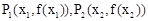 是曲线
是曲线 上的任意两点,要证明
上的任意两点,要证明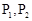 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点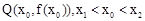 ,使得
,使得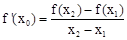 ,且点
,且点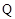 不在
不在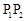 上。 ∵
上。 ∵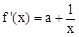 ,即证存在
,即证存在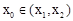 ,使得
,使得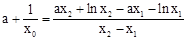 ,
,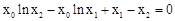 成立,且点
成立,且点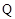 不在
不在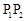 上。…………… 8分
上。…………… 8分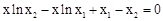 在
在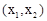 内有解。
内有解。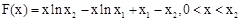 。…
。…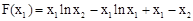 。
。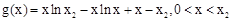 ,
,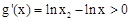 ,
,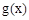 在
在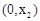 内是增函数,
内是增函数,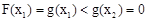 。 同理
。 同理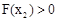 。
。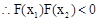 。
。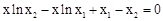 在
在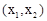 内有解
内有解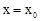 。又对于函数
。又对于函数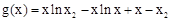 ,
,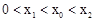 ,
,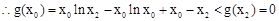 ,
,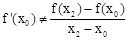 ,即点Q不在
,即点Q不在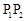 上。
上。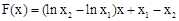 在
在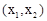 内是增函数,
内是增函数,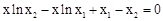 在
在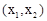 内有唯一解。
内有唯一解。 上任意一条弦均有伴随切线,并且伴随切线是唯一的。
上任意一条弦均有伴随切线,并且伴随切线是唯一的。

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源:不详 题型:解答题
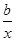 ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
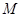 是满足下列性质函数的
是满足下列性质函数的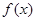 的全体,在定义域
的全体,在定义域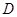 内存在
内存在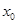 ,使得
,使得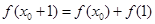 成立。(1)函数
成立。(1)函数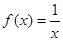 ,
,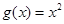 是否属于集合
是否属于集合 ?分别说明理由。(2)若函数
?分别说明理由。(2)若函数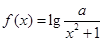 属于集合
属于集合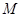 ,求实数
,求实数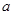 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
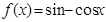 ;②
;②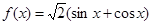 ;③
;③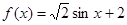 ;④
;④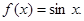 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )| A.①② | B.①③ | C.③④ | D.②④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
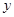 随自变量
随自变量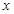 变化的一组数据,由此可判断它最可能的函数模型为
变化的一组数据,由此可判断它最可能的函数模型为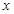 |  |  | 0 | 1 | 2 | 3 |
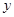 |  |  | 1 | 4 | 16 | 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com