
 ijʳ������ʳ����ʳΪ��ʳ��Ա�����õ��ճ���ʳӦ��������Ҫ̼ˮ������5����λ��������6����λ��֬��6����λ��ÿ����ʳ����7����λ��̼ˮ�����7����λ�ĵ����ʣ�14����λ��֬��������28Ԫ����ÿ����ʳ����7����λ��̼ˮ�����14����λ�ĵ����ʣ�7����λ��֬��������21Ԫ��Ϊ������Ա�����ճ���ʳҪ��ͬʱʹ������ͣ���Ҫͬʱ�ɹ���ʳ����ʳ�����ٷݣ�
ijʳ������ʳ����ʳΪ��ʳ��Ա�����õ��ճ���ʳӦ��������Ҫ̼ˮ������5����λ��������6����λ��֬��6����λ��ÿ����ʳ����7����λ��̼ˮ�����7����λ�ĵ����ʣ�14����λ��֬��������28Ԫ����ÿ����ʳ����7����λ��̼ˮ�����14����λ�ĵ����ʣ�7����λ��֬��������21Ԫ��Ϊ������Ա�����ճ���ʳҪ��ͬʱʹ������ͣ���Ҫͬʱ�ɹ���ʳ����ʳ�����ٷݣ� ���� ��ÿ�칺����ʳx�ݣ���ʳy�ݣ�����Ϊz�������⽨����Ԫһ�β���ʽ��Ϊ$\left\{\begin{array}{l}{7x+7y��5}\\{7x+14y��6}\\{14x+7y��6}\\{x��0}\\{y��0}\end{array}\right.$��Ŀ�꺯��Ϊz=28x+21y���������������ν�Ͽɵã�
���  �⣺��ÿ�칺����ʳx�ݣ���ʳy�ݣ�����Ϊz�������⽨����Ԫһ�β���ʽ��Ϊ$\left\{\begin{array}{l}{7x+7y��5}\\{7x+14y��6}\\{14x+7y��6}\\{x��0}\\{y��0}\end{array}\right.$ ��
�⣺��ÿ�칺����ʳx�ݣ���ʳy�ݣ�����Ϊz�������⽨����Ԫһ�β���ʽ��Ϊ$\left\{\begin{array}{l}{7x+7y��5}\\{7x+14y��6}\\{14x+7y��6}\\{x��0}\\{y��0}\end{array}\right.$ ��
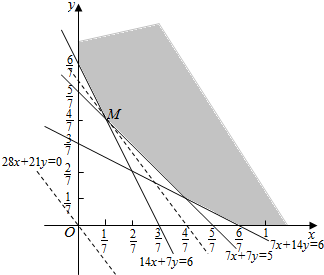
Ŀ�꺯��Ϊz=28x+21y��������Ԫһ�β���ʽ�������ʾ��ƽ��������ͼ��Ӱ���ּ�������
��ͼ��ʾ����ֱ��z=28x+21y�����������ϵĵ�Mʱ���ؾ���С����z��С��
�ⷽ����$\left\{\begin{array}{l}{7x+7y=5}\\{14x+7y=6}\end{array}\right.$����M������Ϊ��$\frac{1}{7}$��$\frac{4}{7}$�����������ɵ�zmin=28x+21y=16��
��ÿ�칺����ʳ$\frac{1}{7}$�ݣ���ʳ$\frac{4}{7}$�ݣ����ܹ������ճ�Ҫ����ʹ������ͣ���ͳɱ�Ϊ16Ԫ��
���� ���⿼������Թ滮��ʵ��Ӧ�ã�������ѧģ�Ͳ�ȷ��ͼ�ǽ������Ĺؼ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
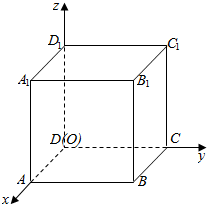 ��ͼ��ʾ����������ABCD-A1B1C1D1�Ķ���DΪ����ԭ��O����ͼ�����ռ�ֱ������ϵ������$\overrightarrow{{A}_{1}C}$���ߵ���������������ǣ�������
��ͼ��ʾ����������ABCD-A1B1C1D1�Ķ���DΪ����ԭ��O����ͼ�����ռ�ֱ������ϵ������$\overrightarrow{{A}_{1}C}$���ߵ���������������ǣ�������| A�� | ��1��$\sqrt{2}$��$\sqrt{2}$�� | B�� | ��1��1��$\sqrt{2}$�� | C�� | ��$\sqrt{2}$��-$\sqrt{2}$��$\sqrt{2}$�� | D�� | ��$\sqrt{2}$��$\sqrt{2}$��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��1} | B�� | {-1��3} | C�� | {1��3} | D�� | {3��1��-1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
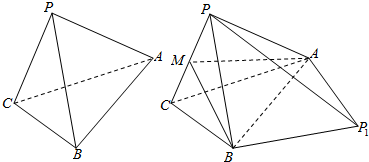 ��ͼ1��������PABC�У�BC=BP=1��AC=AP=$\sqrt{3}$��AB=2������PAB��ֱ��AB��������P1AB��ʹ��A��P1��B��C��ͬһƽ���ڣ���ͼ2������MΪPC�е㣮
��ͼ1��������PABC�У�BC=BP=1��AC=AP=$\sqrt{3}$��AB=2������PAB��ֱ��AB��������P1AB��ʹ��A��P1��B��C��ͬһƽ���ڣ���ͼ2������MΪPC�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ | B�� | ��Ҫ����� | ||
| C�� | ��Ҫ | D�� | �Ȳ����Ҳ����Ҫ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com