
【题目】如图,已知椭圆C:![]() 的离心率为
的离心率为![]() ,并且椭圆经过点P(1,
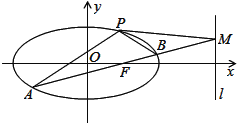
,并且椭圆经过点P(1,![]() ),直线l的方程为x=4.
),直线l的方程为x=4.
(1)求椭圆的方程;
(2)已知椭圆内一点E(1,0),过点E作一条斜率为k的直线与椭圆交于A,B两点,交直线l于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数![]() ,使得k1+k2=
,使得k1+k2=![]() k3?若存在,求出
k3?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】为了调查某野生动物保护区内某种野生动物的数量,调查人员某天逮到这种动物1200只作好标记后放回,经过一星期后,又逮到这种动物1000只,其中作过标记的有100只,按概率的方法估算,保护区内有多少只该种动物.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分).以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界曲线符合函数![]() 模型.园区服务中心P在x轴正半轴上,PO=
模型.园区服务中心P在x轴正半轴上,PO=![]() 百米.
百米.

(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道直线段PQ最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
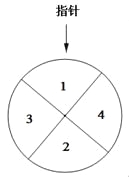
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() 且
且![]() )在区间
)在区间![]() 上的最大值与最小值之和为
上的最大值与最小值之和为![]() ,
,![]() ,其中
,其中![]() .
.
(1)直接写出![]() 的解析式和单调性;
的解析式和单调性;
(2)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若
,若![]() ,使得对
,使得对![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 与圆
与圆![]() 外切于原点
外切于原点![]() ,且两圆圆心的距离
,且两圆圆心的距离![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)过点![]() 的直线
的直线![]() 、
、![]() 与圆
与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() 和点
和点![]() ,与圆
,与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() 和点
和点![]() ,且
,且![]() .求四边形
.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com