Question

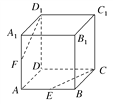
【题目】如图所示，在正方体ABCD－A1B1C1D1中，E为AB的中点，F为AA1的中点．求证：CE，D1F，DA三线交于一点．

Answer 1

【答案】见解析

【解析】试题分析：先证两条直线相交，设交于一点 ，再证交点在第三条直线上，而证交点在第三条直线上，利用两平面的公共点必在这两平面交线上.

试题解析：证明：连接EF，D1C，A1B，

因为E为AB的中点，F为AA1的中点，

所以EF綊A1B.

又因为A1B綊D1C，

所以EF綊D1C，

所以E，F，D1，C四点共面，

可设D1F∩CE＝P.

又D1F平面A1D1DA，CE平面ABCD，

所以点P为平面A1D1DA与平面ABCD的公共点．

又因为平面A1D1DA∩平面ABCD＝DA，

所以据公理3可得P∈DA，即CE，D1F，DA三线交于一点．

点睛;证明线共点问题的方法:先证两条直线交于一点，再证明第三条直线经过该点．