解:(Ⅰ) f(x)的定义域是(-∞,+∞),f′(x)=e
x-a.…2分
(1)当a≤0时,f'(x)>0成立,f(x)的单调增区间为(-∞,+∞); …3分
(2)当a>0时,
令f'(x)>0,得x>lna,则f(x)的单调增区间是(lna,+∞).…4分
令f'(x)<0,得x<lna,则f(x)的单调减区间是(-∞,lna).…5分
综上所述,当a≤0时,f(x)的单调增区间为(-∞,+∞);当a>0时,f(x)的单调增区间是(lna,+∞),单调减区间是(-∞,lna)…6分
(Ⅱ)当x=0时,f(x)=1≥0成立,a∈R.…7分
当x∈(0,+∞)时,f(x)=e
x-ax≥0成立,即x>0 时,

成立.
设
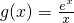
,…9分
所以
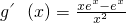
=

.…10分
当x∈(0,1)时,g'(x)<0,函数g(x)在(0,1)上为减函数; …11分
x∈(1,+∞)时,g'(x)>0,函数g(x)在x∈(1,+∞)上为增函数.…12分
则g(x)在x=1处取得最小值,g(1)=e.则a≤e.
综上所述,x∈[0,+∞)时,f(x)≥0成立的a的范围是(-∞,e].…13分
分析:(Ⅰ)先求导,结合函数的定义域,对参数a进行讨论,利用导数大于0得函数的单调增区间,导数小于0得函数的单调减区间;
(Ⅱ)当x=0时,f(x)=1≥0成立;当x∈(0,+∞)时,f(x)=e
x-ax≥0成立,分离参数可得

成立.只需要求右边函数的最小值即可,构建函数
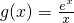
,求导确定函数的单调区间,从而可得函数的最小值,由此可求参数a的范围
点评:本题以函数为载体,考查函数的单调性,考查不等式恒成立问题,考查化归转化思想和分类讨论思想,解题的关键是利用导数大于0,确定单调增区间,导数小于0,确定单调减区间,注意分离参数法在解决恒成立问题中的运用.

 成立.
成立.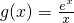 ,…9分
,…9分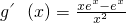 =
= .…10分
.…10分 成立.只需要求右边函数的最小值即可,构建函数
成立.只需要求右边函数的最小值即可,构建函数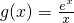 ,求导确定函数的单调区间,从而可得函数的最小值,由此可求参数a的范围
,求导确定函数的单调区间,从而可得函数的最小值,由此可求参数a的范围

 名校课堂系列答案
名校课堂系列答案