
【题目】随着苹果6手机的上市,很多消费者觉得价格偏高,尤其是一部分大学生可望而不可及,因此“国美在线”推出无抵押分期付款购买方式,某分期店对最近100位采用分期付款的购买者进行统计,统计结果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频 数 | 35 | 25 | a | 10 | b |
已知分3期付款的频率为0.15,并且店销售一部苹果6,顾客分1期付款,其利润为1千元;分2期或3期付款,其利润为1.5千元;分4期或5期付款,其利润为2千元,以频率作为概率.
(1)求事件A:“购买的3位顾客中,至多有1位分4期付款”的概率;
(2)用X表示销售一该手机的利润,求X的分布列及数学期望E(x)
【答案】
(1)解:由 ![]() =0.15,得a=15,
=0.15,得a=15,
因为35+25+a+10+b=100,所以b=15,
“购买该手机的3位顾客中至多有1位采用4期付款”的概率:
P(A)= ![]() .
.
(2)解:记分期付款的期数为ξ,依题意得ξ=1,2,3,4,5,
P(ξ=1)=0.35,P(ξ=2)=0.25,P(ξ=3)=0.15,P(ξ=4)=0.1,P(ξ=5)=0.15,
并且P(X=1)=P(ξ=1)=0.35,P(X=2)=P(ξ=4)+P(ξ=5)=0.1+0.15=0.25.
P(X=4)=1﹣0.35﹣0.25=0.4,
所以X的分布列为
X | 1 | 1.5 | 2 |
P | 0.35 | 0.4 | 0.25 |
所以X的数学期望为E(X)=1×0.35+1.5×0.4+2×0.25=1.45(千元)
【解析】(1)由题意得a=15,b=15,由此能求出“购买该手机的3位顾客中至多有1位采用4期付款”的概率.(2)记分期付款的期数为ξ,依题意得ξ=1,2,3,4,5,P(ξ=1)=0.35,P(ξ=2)=0.25,P(ξ=3)=0.15,P(ξ=4)=0.1,P(ξ=5)=0.15,并且P(X=1)=P(ξ=1)=0.35,P(X=2)=P(ξ=4)+P(ξ=5)=0.1+0.15=0.25.P(X=4)=1﹣0.35﹣0.25=0.4,由此能求出X的分布列和数学期望.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
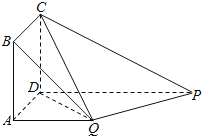
【题目】如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.
(1)证明:平面PQC⊥平面DCQ;
(2)求直线DQ与面PQC成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(1﹣ax)ln(x+1)﹣bx,其中a和b是实数,曲线y=f(x)恒与x轴相切于坐标原点.
(1)求常数b的值;
(2)当a=1时,讨论函数f(x)的单调性;
(3)当0≤x≤1时关于x的不等式f(x)≥0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知命题![]() :实数
:实数![]() 满足
满足![]() ,命题
,命题![]() :实数
:实数![]() 满足方程
满足方程![]() 表示的焦点在
表示的焦点在![]() 轴上的椭圆,且
轴上的椭圆,且![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围;
的取值范围;
(2)设命题![]() :关于
:关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ;
;![]() :函数
:函数![]() 的定义域为
的定义域为![]() .若
.若![]() 是真命题,
是真命题,![]() 是假命题,求实数
是假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)双曲线![]() 的离心率为_____________
的离心率为_____________
(2)点P是椭圆![]() 上一点,
上一点,![]() 分别是椭圆的左、右焦点,若
分别是椭圆的左、右焦点,若![]() ,则
,则![]() 的大小______ .
的大小______ .
(3)如果![]() 是抛物线y2=4x上的点,它们的横坐标依次为
是抛物线y2=4x上的点,它们的横坐标依次为![]() ,F是抛物线的焦点,若
,F是抛物线的焦点,若![]() 则
则![]() _______________.
_______________.
(4)若x,y满足约束条件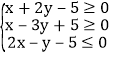 ,则z=x2+y2的最大值为______________.
,则z=x2+y2的最大值为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,右顶点、上顶点分别为点
,右顶点、上顶点分别为点![]() ,
,
已知椭圆![]() 的焦距为
的焦距为![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当
两点,当![]() 面积取得最大时,求直线
面积取得最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣1,1].
(1)求m的值;
(2)若a,b,c∈R,且 ![]() =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com