
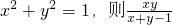 的最大值为________.
的最大值为________.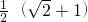
 .由xy=
.由xy=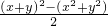 =
=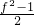 ,知
,知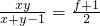 ≤
≤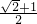 .由此能求出
.由此能求出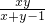 的最大值.
的最大值. ))2-(sin(
))2-(sin( ))2]•2sin(
))2]•2sin( )cos(
)cos( )=sin(
)=sin( )•[cos(
)•[cos( )-sin(
)-sin( )]•(1+cosa+sina),而x+y-1=sina+cosa-1=2sin(
)]•(1+cosa+sina),而x+y-1=sina+cosa-1=2sin( )cos(
)cos( )-2(sin(
)-2(sin( ))2=2sin(
))2=2sin( )•[cos(
)•[cos( )-sin(
)-sin( )],由此能求出
)],由此能求出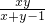 的最大值.
的最大值. .
.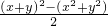 =
=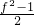 ,
,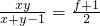 ≤
≤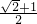 .
. 时,
时,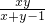 取到最大值
取到最大值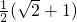 .
. ))2-(sin(
))2-(sin( ))2]•2sin(
))2]•2sin( )cos(
)cos( )
) )•[cos(
)•[cos( )-sin(
)-sin( )]•[cos(
)]•[cos( )+sin(
)+sin( )]•cos(
)]•cos( )
) )•[cos(
)•[cos( )-sin(
)-sin( )]•(1+cosa+sina),
)]•(1+cosa+sina), )cos(
)cos( )-2(sin(
)-2(sin( ))2
))2 )•[cos(
)•[cos( )-sin(
)-sin( )],
)],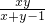 =
= (1+cosa+sina)
(1+cosa+sina) (1+
(1+ sin(a+
sin(a+ ))
)) (1+
(1+ ),
), 时,
时,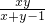 的最大值为
的最大值为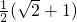 .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源:2013届江苏南京学大教育专修学校高二五月文科数学试卷(解析版) 题型:解答题
已知二次函数 的二次项系数为
的二次项系数为 ,且不等式
,且不等式 的解集为
的解集为 .
.
(1)若方程 有两个相等的实数根, 求
有两个相等的实数根, 求 的解析式;
的解析式;
(2)若 的最大值为正数,求
的最大值为正数,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三第一学期第二次阶段考试数学 题型:解答题
.选修4—4:坐标系与参数方程
椭圆中心在原点,焦点在 轴上。离心率为
轴上。离心率为 ,点
,点 是椭圆上的一个动点,
是椭圆上的一个动点,
若 的最大值为
的最大值为 ,求椭圆的标准方程.
,求椭圆的标准方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com