
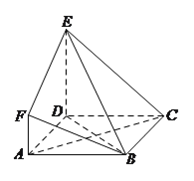
【题目】如图,![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)设点![]() 是线段
是线段![]() 上一个动点,试确定点
上一个动点,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并证明你的结论.
,并证明你的结论.
【答案】(1)见解析(2)![]() (3)点
(3)点![]() 是线段
是线段![]() 靠近
靠近![]() 点的三等分点.
点的三等分点.
【解析】试题分析:(1)由正方形性质得![]() ,由
,由![]() 平面
平面![]() 得
得![]() ,再根据线面垂直判定定理得
,再根据线面垂直判定定理得![]() 平面
平面![]() (2)利用空间向量求二面角:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角关系求二面角(3)设点
(2)利用空间向量求二面角:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,根据向量数量积求向量夹角,最后根据二面角与向量夹角关系求二面角(3)设点![]() 坐标,根据
坐标,根据![]() 平面
平面![]() 得
得![]() ,列方程解得点
,列方程解得点![]() 坐标,再确定位置
坐标,再确定位置
试题解析:(Ⅰ)证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)∵![]() ,
,![]() ,
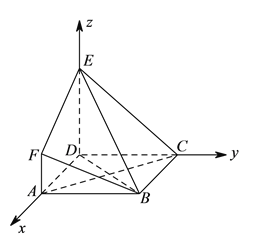
,![]() 两两垂直,所以建立如图空间直角坐标系
两两垂直,所以建立如图空间直角坐标系![]() ,
,
∵![]() 与平面
与平面![]() 所成角为
所成角为![]() ,即
,即![]() ,
,
∴![]() ,
,
由![]() ,可知:
,可知:![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
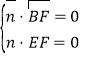 ,即
,即![]() ,
,
令![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的法向量,
的法向量,
∴![]() ,
,
所以![]() .
.
因为二面角为锐角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)依题意得,设![]() ,
,
则![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
此时![]() ,
,
∴点![]() 是线段
是线段![]() 靠近
靠近![]() 点的三等分点.
点的三等分点.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】如图,在棱台ABC﹣FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点, ![]() .
. 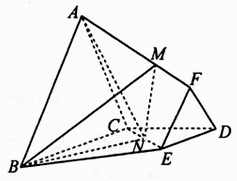
(Ⅰ)λ为何值时,MN∥平面ABC?
(Ⅱ)在(Ⅰ)的条件下,求直线AN与平面BMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCFE中,四边形EFCB为梯形,EF∥BC,且EF= ![]() BC,△ABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG=
BC,△ABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG= ![]() ,CF=
,CF= ![]() ,BF=
,BF= ![]() .
. 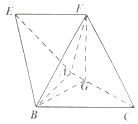
(1)证明:平面FGB⊥平面ABC;
(2)求二面角E﹣AB﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() ,
,![]() 边上的中线
边上的中线![]() 所在的直线方程为
所在的直线方程为![]() ,
,![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() .
.
(![]() )求
)求![]() 的顶点
的顶点![]() 、
、![]() 的坐标.
的坐标.
(![]() )若圆
)若圆![]() 经过不同的三点
经过不同的三点![]() 、
、![]() 、
、![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司进行仓储机器人升级换代期间,第一年有机器人![]() 台,平均每台机器人创收利润
台,平均每台机器人创收利润![]() 万元.预测以后每年平均每台机器人创收利润都比上一年增加
万元.预测以后每年平均每台机器人创收利润都比上一年增加![]() 万元,但该物流公司在用机器人数量每年都比上一年减少
万元,但该物流公司在用机器人数量每年都比上一年减少![]() .
.
(1)设第![]() 年平均每台机器人创收利润为
年平均每台机器人创收利润为![]() 万元,在用机器人数量为
万元,在用机器人数量为![]() 台,求
台,求![]() ,
,![]() 的表达式;
的表达式;
(2)依上述预测,第几年该物流公司在用机器人创收的利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣alnx﹣(a﹣2)x.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)有两个零点x1 , x2(1)求满足条件的最小正整数a的值;
(Ⅲ)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量![]() (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当![]() 时,为酒后驾车;当
时,为酒后驾车;当![]() 时,为醉酒驾车.某市交通管理部门于某天晚上8点至11点设点进行一次拦查行动,共依法查出60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中
时,为醉酒驾车.某市交通管理部门于某天晚上8点至11点设点进行一次拦查行动,共依法查出60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中![]() 的人数计入
的人数计入![]() 人数之内).
人数之内).

1)求此次拦查中醉酒驾车的人数;
2)从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究,再从抽取的8人中任取2人,求两人中恰有1人醉酒驾车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题计结果如下图表所示:
人,回答问题计结果如下图表所示:

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com