
【题目】我们称满足以下两个条件的有穷数列![]() 为
为![]() 阶“期待数列”;①
阶“期待数列”;①![]() ;②
;②![]() .
.
(1)若数列![]() 的通项公式是
的通项公式是![]() ,试判断数列
,试判断数列![]() 是否为2014阶“期待数列”,并说明理由;
是否为2014阶“期待数列”,并说明理由;
(2)若等比数列![]() 为
为![]() 阶“期待数列”,求公比
阶“期待数列”,求公比![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(3)若一个等差数列![]() 既是(
既是(![]() )阶“期待数列”又是递增数列,求该数列的通项公式.
)阶“期待数列”又是递增数列,求该数列的通项公式.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() ,圆
,圆![]() :
: ![]() 的圆心
的圆心![]() 在椭圆上,点
在椭圆上,点![]() 到椭圆
到椭圆![]() 的右焦点的距离为
的右焦点的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,且
,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() 为
为![]() 的中点,求
的中点,求![]() 面积的取值范围.
面积的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:x2+y2﹣4x﹣6y+12=0相交于M、N两点
(1)求实数k的取值范围;
(2)求证:![]() 为定值;
为定值;
(3)若O为坐标原点,问是否存在直线l,使得![]() ,若存在,求直线l的方程,若不存在,说明理由.
,若存在,求直线l的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q,并修建两段直线型道路PB、QA.规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).

(1)若道路PB与桥AB垂直,求道路PB的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)对规划要求下,若道路PB和QA的长度均为d(单位:百米).求当d最小时,P、Q两点间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在x轴上的椭圆C1的长轴长为8,短半轴为2![]() ,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点.
,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点.
(1)求抛物线C2的标准方程;
(2)过(1,0)的两条相互垂直的直线与抛物线C2有四个交点,求这四个点围成四边形的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果四面体的四条高交于一点,则该点称为四面体的垂心,该四面体称为垂心四面体.
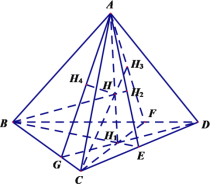
(1)证明:如果四面体的对棱互相垂直,则该四面体是垂心四面体;反之亦然.
(2)给出下列四面体
①正三棱锥;
②三条侧棱两两垂直;
③高在各面的射影过所在面的垂心;
④对棱的平方和相等.
其中是垂心四面体的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温情况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:

①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差小于乙地该月14时的平均气温的标准差;
④甲地该月14时的平均气温的标准差大于乙地该月14时的平均气温的标准差,
其中根据茎叶图能得到的统计结论的编号为( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器生产某种产品,如果生产出一件甲等品可获利50元,生产出一件乙等品可获利30元,生产出一件次品,要赔20元,已知这台机器生产出甲等品、乙等品和次品的概率分别为0.6,0.3,和0.1,则这台机器每生产一件产品平均预期可获利________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com