练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数，且
    (1)求；
    (2)判断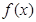的奇偶性；
    (3)判断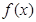在上的单调性，并证明。

    （1）； (2)为偶函数；(3)在单调递减。

    解析试题分析：（1）.,      解得：
    (2)，定义域为
     ，所以为偶函数
    (3)
    由，，则，则在单调递减
    考点：指数函数的性质，函数的奇偶性、单调性，应用导数研究函数的单调性。
    点评：中档题，本题解答思路明确，通过布列方程组求得a,b的值。判断函数的奇偶性，主要应用奇偶函数的定义。在某区间，导数值非负，函数为增函数，导数值非正，函数为减函数。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝|2x－1|＋|2x＋a|，g(x)=x+3.
    （Ⅰ）当a=-2时，求不等式f(x)＜g(x)的解集；
    （Ⅱ）设a＞－1，且当x∈[，)时，f(x)≤g(x)，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设.
    （1）求函数的单调区间；
    （2）若当时恒成立，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    探究函数f（x）=x＋,x∈（0，+∞）的最小值,并确定取得最小值时x的值.列表如下：

    x
    		…
    		0.5
    		1
    		1.5
    		1.7
    		1.9
    		2
    		2.1
    		2.2
    		2.3
    		3
    		4
    		5
    		7
    		…
    y
    		…
    		8.5
    		5
    		4.17
    		4.05
    		4.005
    		4
    		4.005
    		4.02
    		4.04
    		4.3
    		5
    		5.8
    		7.57
    		…
    请观察表中y值随x值变化的特点,完成以下的问题.
    函数f（x）=x＋（x＞0）在区间（0,2）上递减；
    （1）函数f（x）=x＋（x＞0）在区间                  上递增.
    当x=                 时,y最小=                         .
    （2）证明：函数f（x）=x＋在区间（0,2）上递减.
    （3）思考：函数f（x）=x＋（x＜0）有最值吗？如果有,那么它是最大值还是最小值？此时x为何值？（直接回答结果,不需证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数，，其中．
    （1）若是函数的极值点，求实数的值；
    （2）若对任意的（为自然对数的底数）都有≥成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数满足，其中a>0,a≠1．
    （1）对于函数，当x∈（-1,1）时，f（1-m）+f（1-m2）<0,求实数m的取值集合；
    （2）当x∈（-∞,2）时，的值为负数，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数
    （1）若，求在图象与轴交点处的切线方程；
    （2）若在（1，2）上为单调函数，求的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设有极值，
    （Ⅰ）求的取值范围；
    （Ⅱ）求极大值点和极小值点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题


    设命题p：函数的定义域为R；命题q：不等式对任意恒成立．
    （Ⅰ）如果p是真命题，求实数的取值范围；
    （Ⅱ）如果命题“p或q”为真命题且“p且q”为假命题，求实数的取值范围．

    查看答案和解析>>

    同步练习册答案