
【题目】已知函数f(x)=x3+ax2+bx-a2-7a在x=1处取得极大值10,则![]() 的值为( )
的值为( )
A. -![]() B. -2
B. -2
C. -2或-![]() D. 2或-
D. 2或-![]()
【答案】A
【解析】∵f(x)=x3+ax2+bx﹣a2﹣7a,
∴f′(x)=3x2+2ax+b,
又f(x)=x3+ax2+bx﹣a2﹣7a在x=1处取得极大值10,
∴f′(1)=3+2a+b=0,f(1)=1+a+b﹣a2﹣7a=10,
∴a2+8a+12=0,
∴a=﹣2,b=1或a=﹣6,b=9.
当a=﹣2,b=1时,f′(x)=3x2﹣4x+1=(3x﹣1)(x﹣1),
当![]() <x<1时,f′(x)<0,当x>1时,f′(x)>0,
<x<1时,f′(x)<0,当x>1时,f′(x)>0,
∴f(x)在x=1处取得极小值,与题意不符;
当a=﹣6,b=9时,f′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3)
当x<1时,f′(x)>0,当1<x<3时,f′(x)<0,
∴f(x)在x=1处取得极大值,符合题意;
∴![]() =﹣
=﹣![]() .
.
故选A.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 点
点![]() ,
, ![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() 。
。
(Ⅰ)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)直线![]() 与点
与点![]() 的轨迹交于不同两点
的轨迹交于不同两点![]() 和
和![]() ,且
,且![]() (其中 O 为坐标
(其中 O 为坐标
原点),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1的底面是边长为4的正三角形,AA1⊥平面ABC,AA1=2![]() ,M为A1B1的中点.
,M为A1B1的中点.
(1)求证:MC⊥AB;
(2)在棱CC1上是否存在点P,使得MC⊥平面ABP?若存在,确定点P的位置;若不存在,说明理由.
(3)若点P为CC1的中点,求二面角B-AP-C的余弦值.
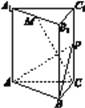
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx-x+a+1.
(1)若存在x∈(0,+∞),使得f(x)≥0成立,求a的取值范围;
(2)求证:在(1)的条件下,当x>1时, ![]() x2+ax-a>xlnx+
x2+ax-a>xlnx+![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.

(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
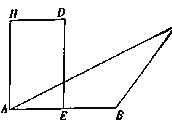
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 垂直平分线上的一点,且
垂直平分线上的一点,且![]() ,四边形
,四边形![]() 为矩形,固定边
为矩形,固定边![]() ,在平面
,在平面![]() 内移动顶点
内移动顶点![]() ,使得
,使得![]() 的内切圆始终与
的内切圆始终与![]() 切于线段
切于线段![]() 的中点,且
的中点,且![]() 在直线
在直线![]() 的同侧,在移动过程中,当
的同侧,在移动过程中,当![]() 取得最小值时,点
取得最小值时,点![]() 到直线
到直线![]() 的距离为__________.
的距离为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
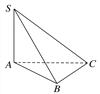
【题目】如图所示,在三棱锥S—ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=3a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com