
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以原点为圆心,以短轴长为直径的圆
,且以原点为圆心,以短轴长为直径的圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]()
![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且与圆
,且与圆![]() 没有公共点,设
没有公共点,设![]() 为椭圆
为椭圆![]() 上一点,满足
上一点,满足![]() (
(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某公司订购了一批树苗,为了检测这批树苗是否合格,从中随机抽测100株树苗的高度,经数据处理得到如图(1)所示的频率分布直方图,其中最高的16株树苗的高度的茎叶图如图(2)所示,以这100株树苗的高度的频率估计整批树苗高度的概率.
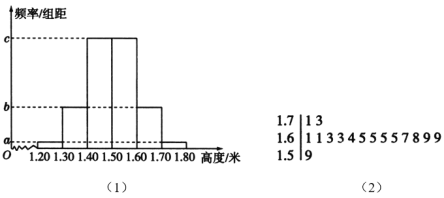
(1)求这批树苗的高度高于![]() 米的概率,并求图(1)中
米的概率,并求图(1)中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若从这批树苗中随机选取3株,记![]() 为高度在
为高度在![]() 的树苗数量,求
的树苗数量,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果这批树苗的高度满足近似于正态分布
的概率分布.如果这批树苗的高度满足近似于正态分布![]() 的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗能否被签收?
的概率分布,则认为这批树苗是合格的,将顺利被签收,否则,公司将拒绝签收.试问:该批树苗能否被签收?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,
,![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,坐标原点O到直线
,坐标原点O到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆C的方程;
(2)过椭圆C上一点P作两条直线,分别与椭圆C相交于异于点P的点A,B,若四边形![]() 为平行四边形,探究四边形
为平行四边形,探究四边形![]() 的面积是否为定值.若是,求出此定值;若不是,请说明理由.
的面积是否为定值.若是,求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加竞答游戏,一轮三个题目,每人回答一题为体现公平,制定如下规则:
①第一轮回答顺序为甲、乙、丙;第二轮回答顺序为乙、丙、甲;第三轮回答顺序为丙,甲、乙;第四轮回答顺序为甲、乙、丙;…,后面按此规律依次向下进行;
②当一人回答不正确时,竞答结束,最后一个回答正确的人胜出.
已知,每次甲回答正确的概率为![]() ,乙回答正确的概率为
,乙回答正确的概率为![]() ,丙回答正确的概率为
,丙回答正确的概率为![]() ,三个人回答每个问题相互独立.
,三个人回答每个问题相互独立.
(1)求一轮中三人全回答正确的概率;
(2)分别求甲在第一轮、第二轮、第三轮胜出的概率;
(3)记![]() 为甲在第
为甲在第![]() 轮胜出的概率,
轮胜出的概率,![]() 为乙在第
为乙在第![]() 轮胜出的概率,求
轮胜出的概率,求![]() 与
与![]() ,并比较
,并比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
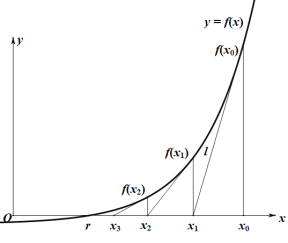
【题目】牛顿迭代法(Newtonsmethod)又称牛顿-拉夫逊方法(Newton-Raphsonmethod),是牛顿在17世纪提出的一种近似求方程根的方法.如图,设![]() 是
是![]() 的根,选取
的根,选取![]() 作为
作为![]() 初始近似值,过点
初始近似值,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
,![]() 与
与![]() 轴的交点的横坐标
轴的交点的横坐标![]() ,称
,称![]() 是
是![]() 的一次近似值,过点
的一次近似值,过点![]() 作曲线
作曲线![]() 的切线,则该切线与
的切线,则该切线与![]() 轴的交点的横坐标为
轴的交点的横坐标为![]()
![]() ,称
,称![]() 是
是![]() 的二次近似值.重复以上过程,得到
的二次近似值.重复以上过程,得到![]() 的近似值序列.请你写出
的近似值序列.请你写出![]() 的
的![]() 次近似值与
次近似值与![]() 的
的![]() 次近似值的关系式______,若
次近似值的关系式______,若![]() ,取
,取![]() 作为
作为的初始近似值,试求
![]() 的一个根
的一个根![]() 的三次近似值______(请用分数做答).
的三次近似值______(请用分数做答).
查看答案和解析>>
科目:高中数学 来源: 题型:
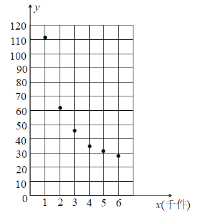
【题目】2020年初全球爆发了新冠肺炎疫情,为了防控疫情,某医疗科研团队攻坚克难研发出一种新型防疫产品,该产品的成本由原料成本及非原料成本组成,每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,根据已经生产的统计数据,绘制了如下的散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用函数![]() 对两个变量的关系进行拟合.参考数据(其中
对两个变量的关系进行拟合.参考数据(其中![]() ):
):
|
|
|
|
|
|
|
0.41 | 0.1681 | 1.492 | 306 | 20858.44 | 173.8 | 50.39 |
(1)求y关于x的回归方程,并求y关于u的相关系数(精确到0.01).
(2)该产品采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为80元,则签订9千件订单的概率为0.7,签订10千件订单的概率为0.3;若单价定为70元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为30元,根据(1)的结果,要想获得更高利润,产品单价应选择80元还是70元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,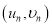 ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: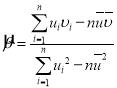 ,
,![]() ,相关系数
,相关系数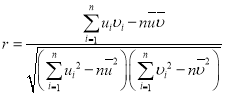 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com