
【题目】定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y![]() ,有
,有![]() ,f(1)=2,且
,f(1)=2,且![]() .
.
(1)求f(0)的值;
(2)求证:对任意x![]() ,都有f(x)>0;
,都有f(x)>0;
(3)解不等式f(3![]() 2x)>4.
2x)>4.
【答案】(1) f(0)=1.(2)证明见解析;(3) ![]()
【解析】
(1)利用赋值法,先令![]() 以及令
以及令![]() ,由此解得
,由此解得![]() 的值.(2)首先利用
的值.(2)首先利用![]() 结合已知条件证得
结合已知条件证得![]() ,再利用反证法,证得
,再利用反证法,证得![]() ,由此证得
,由此证得![]() 成立.(3)利用赋值法,将
成立.(3)利用赋值法,将![]() 转化为
转化为![]() ,通过证明函数
,通过证明函数![]() 为
为![]() 上的增函数,由求得不等式的解集.
上的增函数,由求得不等式的解集.
(1)对任意![]() ,
,![]() .
.
令x=y=0,得f(0)=f(0)·f(0),即f(0)·[f(0)![]() 1]=0.
1]=0.
令y=0,得f(x)=f(x)·f(0),对任意x![]() 成立,
成立,
所以f(0)≠0,因此f(0)=1.
(2)证明:对任意x![]() ,有
,有 .
.
假设存在x0![]() ,使f(x0)=0,
,使f(x0)=0,
则对任意x>0,有f(x)=f[(x![]() x0)+x0]=f(x
x0)+x0]=f(x![]() x0)·f(x0)=0.
x0)·f(x0)=0.
这与已知x>0时,f(x)>1矛盾.所以,对任意x![]() ,均有f(x)>0成立.
,均有f(x)>0成立.
(3)令x=y=1有f(1![]() 1)=f(1)·f(1),
1)=f(1)·f(1),
所以f(2)=2×2=4.任取x1,x2![]() ,且x1<x2,
,且x1<x2,
则f(x2)-f(x1)=f[(x2![]() x1)+x1]
x1)+x1]![]() f(x1)=f(x2
f(x1)=f(x2![]() x1)·f(x1)
x1)·f(x1) ![]() f(x1)=f(x1)·[f(x2
f(x1)=f(x1)·[f(x2![]() x1)
x1)![]() 1].
1].
∵x1<x2,∴x2![]() x1>0,由已知f(x2
x1>0,由已知f(x2![]() x1)>1,∴f(x2
x1)>1,∴f(x2![]() x1)
x1)![]() 1>0.
1>0.
由(2)知x1![]() ,f(x1)>0.所以f(x2)
,f(x1)>0.所以f(x2)![]() f(x1)>0,即f(x1)<f(x2).
f(x1)>0,即f(x1)<f(x2).
故函数f(x)在![]() 上是增函数.
上是增函数.
由f(3![]() 2x)>4,得f(3
2x)>4,得f(3![]() 2x)>f(2),即3
2x)>f(2),即3![]() 2x>2.解得x<
2x>2.解得x<![]() .
.
所以,不等式的解集是![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( )
内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为![]() ,且各件产品是否为不合格品相互独立.
,且各件产品是否为不合格品相互独立.
(1)记20件产品中恰有2件不合格品的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() .
.
(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的![]() 作为
作为![]() 的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为![]() ,求
,求![]() ;
;
(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.
(1)求开始第4次发球时,甲、乙的比分为1比2的概率;
(2)ξ表示开始第4次发球时乙的得分,求ξ的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() ,记M的轨迹为曲线C.
,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)过坐标原点O的直线l交C于P、Q两点,点P在第一象限,![]() 轴,垂足为H.连结QH并延长交C于点R.
轴,垂足为H.连结QH并延长交C于点R.
(i)设O到直线QH的距离为d.求d的取值范围;
(ii)求![]() 面积的最大值及此时直线l的方程.
面积的最大值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥的底面是边长为![]() 的正方形,侧棱长均为
的正方形,侧棱长均为![]() ,若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的侧面积为________.
,若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的侧面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在充分竞争的市场环境中,产品的定价至关重要,它将影响产品的销量,进而影响生产成本、品牌形象等![]() 某公司根据多年的市场经验,总结得到了其生产的产品A在一个销售季度的销量
某公司根据多年的市场经验,总结得到了其生产的产品A在一个销售季度的销量![]() 单位:万件
单位:万件![]() 与售价
与售价![]() 单位:元
单位:元![]() 之间满足函数关系
之间满足函数关系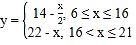 ,A的单件成本
,A的单件成本![]() 单位:元
单位:元![]() 与销量y之间满足函数关系
与销量y之间满足函数关系![]() .
.
![]() 当产品A的售价在什么范围内时,能使得其销量不低于5万件?
当产品A的售价在什么范围内时,能使得其销量不低于5万件?
![]() 当产品A的售价为多少时,总利润最大?
当产品A的售价为多少时,总利润最大?![]() 注:总利润
注:总利润![]() 销量
销量![]() 售价
售价![]() 单件成本
单件成本![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,新街口某新开业的商场在过去一个月内(以30天计),顾客人数![]() (千人)与时间
(千人)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]() (
(![]() ),人均消费
),人均消费![]() (元)与时间
(元)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]()
(1)求该商场的日收益![]() (千元)与时间
(千元)与时间![]() (天)(
(天)(![]() ,
, ![]() )的函数关系式;
)的函数关系式;
(2)求该商场日收益的最小值(千元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数),设![]() ,
,
(1)若f(-1)=0,且对任意实数x均有f(x)≥0成立,求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)满足f(-x)=f(x),试比较F(m)+F(n)的值与0的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com