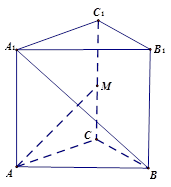
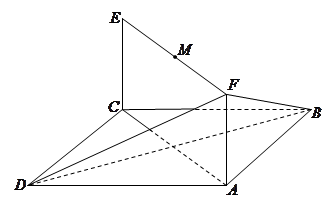在长方体
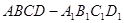
中,AB=BC=2,
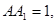
则
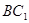
与面
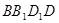
所成角的正弦值为( )
解:连接A
1C
1交B
1D
1于O,连接BO,则
∵长方体
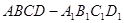
中,AB=BC=2
∴C
1O⊥平面BD B
1D
1∴∠C
1BO为BC
1与平面BD B
1D
1所成角
∵C
1O=
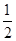
A
1C
1=" 2" ,BC
1=
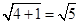
∴sin∠C
1BO=C
1O: BC
1 =
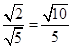
故答案为:
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
如图,在三棱拄

中,

侧面

,已知



(1)求证:

;(4分)
(2)、当

为

的中点时,求二面角

的平面角的正切值.(8分)
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
若
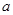
、
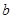
是直线,
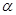
、
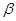
是平面,
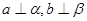
,向量
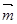
在
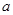
上,向量
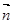
在
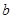
上,
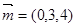
,
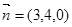
,则
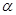
、
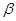
所成二面角中较小的一个余弦值为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
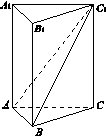
在正三棱柱
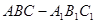
中,AB=1,若二面角
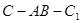
的大小为60°,则点
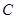
到平面
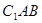
的距离为 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知直线

与平面

所成的角为30°,

为空间一定点,过

作与

、

所成的角都是45°的直线

,则这样的直线

可作( )条
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,已知平行四边形
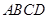
和矩形

所在的平面互相垂直,
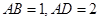
,
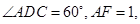
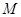
是线段
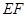
的中点.
(Ⅰ)求二面角
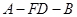
的正弦值;
(Ⅱ)设点
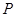
为一动点,若点
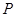
从
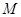
出发,沿棱按照
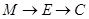
的路线运动到点
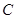
,求这一过程中形成的三棱锥
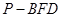
的体积的最小值.
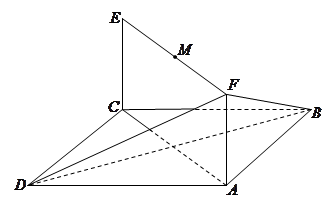
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
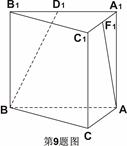
如图所示,
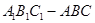
是直三棱柱,
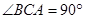
,点
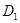
、
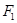
分别是
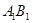
,
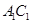
的中点,若
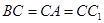
,则
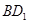
与
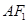
所成角的余弦值是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,在直三棱柱
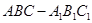
中,
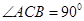
,
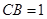
,
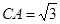
,
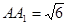
,
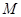
为侧棱
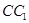
上一点,且
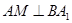
。
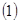
求证:
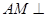
平面
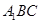
;
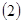
求二面角
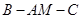
的大小。
查看答案和解析>>

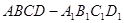 中,AB=BC=2,
中,AB=BC=2,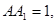 则
则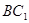 与面
与面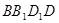 所成角的正弦值为( )
所成角的正弦值为( )

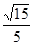

 阅读快车系列答案
阅读快车系列答案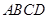 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,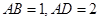 ,
,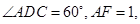
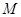 是线段
是线段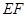 的中点.
的中点.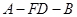 的正弦值;
的正弦值;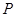 为一动点,若点
为一动点,若点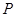 从
从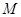 出发,沿棱按照
出发,沿棱按照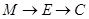 的路线运动到点
的路线运动到点 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥 的体积的最小值.
的体积的最小值.