设函数

.
(1)证明:

;
(2)设

为

的一个极值点,证明
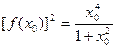
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知定义在R上的函数

,
定义:

.

(1)若

,当

时比较

与

的大小关系.
(2)若对任意的
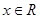
,都有使得

,用反证法证明:

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
请先阅读:
在等式
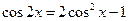
(
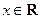
)的两边求导,得:
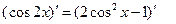
,
由求导法则,得
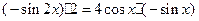
,化简得等式:
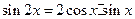
。
(1)利用上题的想法(或其他方法),结合等式
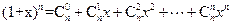
(
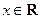
,正整数
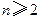
),证明:
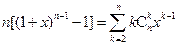
。
(2)对于正整数
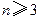
,求证:
(i)
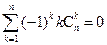
; (ii)
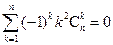
; (iii)
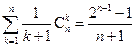
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知

,是否存在不小于2的正整数
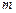
,使得对于任意的正整数

都能被
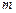
整除?如果存在,求出最大的
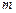
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列{a
n}中,S
n是它的前n项和,并且S
n+1=4a
n+2(n=1,2,…),a
1=1.
(1)设b
n=a
n+1-2a
n(n=1,2,…),求证:数列{b
n}是等比数列;
(2)设c
n=
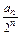
(n=1,2,…),求证:数列{c
n}是等差数列;
(3)求数列{a
n}的通项公式及前n项和公式.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
对任意复数

、

,定义

,其中

是

的共轭复数.对任意复数

、

、

,有如下四个命题:
①

;
②

;
③

;
④

.
则真命题的个数是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
当
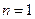
时,有
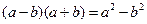
当
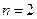
时,有
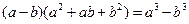
当
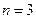
时,有
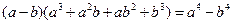
当
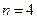
时,有
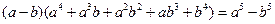
当
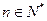
时,你能得到的结论是:
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题

用反证法证明命题“
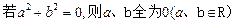
”,其反设正确的是
查看答案和解析>>

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案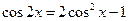 (
(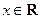 )的两边求导,得:
)的两边求导,得: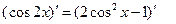 ,
,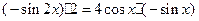 ,化简得等式:
,化简得等式: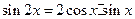 。
。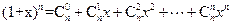 (
(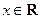 ,正整数
,正整数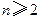 ),证明:
),证明: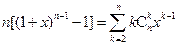 。
。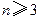 ,求证:
,求证: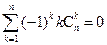 ; (ii)
; (ii)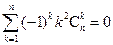 ; (iii)
; (iii)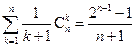 。
。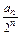 (n=1,2,…),求证:数列{cn}是等差数列;
(n=1,2,…),求证:数列{cn}是等差数列;