
【题目】设函数![]() (
(![]() 且
且![]() ,
,![]() ),
),![]() 是定义域是
是定义域是![]() 的奇函数.
的奇函数.
(1)求![]() 的值,判断并证明当
的值,判断并证明当![]() 时,函数
时,函数![]() 在
在![]() 上的单调性;
上的单调性;
(2)已知![]() ,函数
,函数![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(3)已知![]() ,若
,若![]() 对于
对于![]() 时恒成立,请求出最大的整数
时恒成立,请求出最大的整数![]()
【答案】(1) ![]() ,
,![]() 在
在![]() 上为增函数;(2)
上为增函数;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】
试题分析:(1)根据函数![]() 为
为![]() 上的奇函数,可得
上的奇函数,可得![]() 的值.即可得
的值.即可得![]() 的解析式,根据函数单调性定义,利用做差可得出函数单调性;(2)根据
的解析式,根据函数单调性定义,利用做差可得出函数单调性;(2)根据![]() 的值求
的值求![]() ,可得
,可得![]() 的解析式,利用换元法,将
的解析式,利用换元法,将![]() 转化为二次函数,利用二次函数的性质,即可求得值域;(3)利用换元法和参变量分离,将不等式转化为恒成立,利用二次函数性质求得最小值,即可求
转化为二次函数,利用二次函数的性质,即可求得值域;(3)利用换元法和参变量分离,将不等式转化为恒成立,利用二次函数性质求得最小值,即可求![]() 范围.
范围.
试题解析:解:
(1)∵![]() 是定义域为
是定义域为![]() 上的奇函数,∴
上的奇函数,∴![]() ,得
,得![]() ,
,
![]() ,
,![]() ,即
,即![]() 是
是![]() 上的奇函数
上的奇函数
设![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上为增函数.
上为增函数.
(2)∵![]() ,∴
,∴![]() ,即
,即![]() ,∴
,∴![]() 或
或![]() (舍去)
(舍去)
则![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,
由(1)可知该函数在区间![]() 上为增函数,则
上为增函数,则![]() ,
,
则![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
所以![]() 的值域为
的值域为![]() .
.
(3)由题意,即![]() ,在
,在![]() 时恒成立,
时恒成立,
令![]() ,
,![]() ,则
,则![]()
则![]() ,
,![]() 恒成立,
恒成立,
即为![]() ,
,![]() 恒成立
恒成立
![]() ,
,![]() 恒成立,当
恒成立,当![]() 时,
时,![]() ,
,
∴![]() ,则
,则![]() 的最大整数为
的最大整数为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”则乙的卡片上的数字是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面几何中,与三角形的三条边所在直线的距离相等的点有4个,类似的,在立体几何中,与四面体的四个面所在平面的距离相等的点有( )
A.1个B.5个C.7个D.9个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的定义域为集合A,B={x|x<a}.
的定义域为集合A,B={x|x<a}.
(1)若AB,求实数a的取值范围;
(2)若全集U={x|x≤4},a=﹣1,求UA及A∩(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在三棱锥![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() 都是正三角形,
都是正三角形,![]() .
.
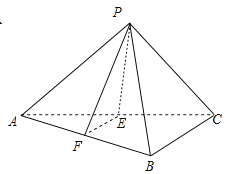
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)若点![]() 在一个表面积为
在一个表面积为![]() 的球面上,求
的球面上,求![]() 的边长.
的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装制造商现有300m2的棉布料,900m2的羊毛料,和600 m2的丝绸料。做一条大衣需要1m2的棉布料,5m2的羊毛料,1m2的丝绸料.做一条裤子需要1m2的棉布料,2m2的羊毛料,1m2的丝绸料。
(1)在此基础上生产这两种服装,列出满足生产条件的数学关系式,并在直角坐标系中画出相应的平面区域。
(2)若生产一条大衣的纯收益是120元,生产一条裤子的纯收益是80元,那么应采用哪种生产安排,该服装制造商能获得最大的纯收益;最大收益是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下命題:
①命题 “在![]() 中,若
中,若![]() ,则
,则![]() ” 的逆命題为真命题;
” 的逆命題为真命题;
②若动点![]() 到两定点
到两定点![]() 的距离之和为
的距离之和为![]() ,则动点
,则动点![]() 的轨迹为线段
的轨迹为线段![]() ;
;
③若![]() 为假命题,则
为假命题,则![]() 都是假命題;
都是假命題;
④设![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
⑤若实数![]() 成等比数列,则圆锥曲线
成等比数列,则圆锥曲线![]() 的离心率为
的离心率为![]() ;
;
其中所有正确命题的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的从高气温,下面的折线代表可能出现的最低气温.

(Ⅰ)指出最高气温与最低气温的相关性;
(Ⅱ)估计在10:00时最高气温和最低气温的差;
(Ⅲ)比较最低气温与最高气温方差的大小(结论不要求证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com