
【题目】如图,四棱锥![]() 的一个侧面
的一个侧面![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() .
.
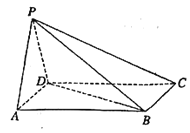
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】
对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时 ①求f0(x)和fk(x)的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
(2)若Φ(x)=x2,则是否存在正整数k,使得不等式fk(x)<(1-3k)x+4k2+3k-1有解?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的![]() ,对教师管理水平给出好评的学生人数为总数的
,对教师管理水平给出好评的学生人数为总数的![]() ,其中对教师教学水平和教师管理水平都给出好评的有120人.
,其中对教师教学水平和教师管理水平都给出好评的有120人.
(1)填写教师教学水平和教师管理水平评价的![]() 列联表:
列联表:
对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
对教师教学水平好评 | |||
对教师教学水平不满意 | |||
合计 |
请问是否可以在犯错误概率不超过0.001的前提下,认为教师教学水平好评与教师管理水平好评有关?
(2)若将频率视为概率,有4人参与了此次评价,设对教师教学水平和教师管理水平全好评的人数为随机变量![]() .
.
①求对教师教学水平和教师管理水平全好评的人数![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②求![]() 的数学期望和方差.
的数学期望和方差.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() 千米,汽车从
千米,汽车从![]() 地匀速行驶到
地匀速行驶到![]() 地,速度不超过
地,速度不超过![]() 千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度
千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度![]() 的平方成正比,比例系数为
的平方成正比,比例系数为![]() ,固定部分为
,固定部分为![]() 元,
元,
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米小时)的函效:并求出当
(千米小时)的函效:并求出当![]() 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;
(2)随着汽车的折旧,运输成本会发生一些变化,那么当![]() ,此时汽车的速度应调整为多大,才会使得运输成本最小,
,此时汽车的速度应调整为多大,才会使得运输成本最小,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对相关系数r来说,下列说法正确的是( ).
A.![]() ,
,![]() 越接近0,相关程度越大;
越接近0,相关程度越大;![]() 越接近1,相关程度越小
越接近1,相关程度越小
B.![]() ,
,![]() 越接近1,相关程度越大;
越接近1,相关程度越大;![]() 越大,相关程度越小
越大,相关程度越小
C.![]() ,
,![]() 越接近1,相关程度越大;
越接近1,相关程度越大;![]() 越接近0,相关程度越小
越接近0,相关程度越小
D.![]() ,
,![]() 越接近1,相关程度越小;
越接近1,相关程度越小;![]() 越大,相关程度越大
越大,相关程度越大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年高考刚过,为了解考生对全国2卷数学试卷难度的评价,随机抽取了某学校50名男考生与50名女考生,得到下面的列联表:
非常困难 | 一般 | |
男考生 | 20 | 30 |
女考生 | 40 | 10 |
(1)分别估计该学校男考生、女考生觉得全国2卷数学试卷非常困难的概率;
(2)从该学校随机抽取3名男考生,2名女考生,求恰有4名考生觉得全国2卷数学试卷非常困难的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com