
【题目】某工厂生产部门随机抽测生产某种零件的工人的日加工零件数(单位:件),其中A车间13人,B车间12人,获得数据如下:

根据上述数据得到样本的频率分布表如下:
分组 | 频数 | 频率 |
[25,30] | 3 | 0.12 |
(30,35] | 5 | 0.20 |
(35,40] | 8 | 0.32 |
(40,45] | n1 | f1 |
(45,50] | n2 | f2 |
(1)确定样本频率分布表中n1、n2、f1和f2的值;
(2)现从日加工零件数落在(40,45]的工人中随机选取两个人,求这两个人中至少有一个来自B车间的概率.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD的底面是边长为a的棱形,PD⊥底面ABCD.

(1)证明:AC⊥平面PBD;
(2)若PD=AD,直线PB与平面ABCD所成的角为45°,四棱锥P—ABCD的体积为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,已知b=1,c=2且2cosA(bcosC+ccosB)=a,则A=__________;若M为边BC的中点,则|AM|=__________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 若该大学某女生身高为170cm,则可断定其体重必为![]()
B. 回归直线过样本点的中心![]()
C. 若该大学某女生身高增加1cm,则其体重约增加![]()
D. y与x具有正的线性相关关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,有正弦定理:
中,有正弦定理:![]() 定值,这个定值就是
定值,这个定值就是![]() 的外接圆的直径
的外接圆的直径![]() 如图2所示,
如图2所示,![]() 中,已知
中,已知![]() ,点M在直线EF上从左到右运动
,点M在直线EF上从左到右运动![]() 点M不与E、F重合
点M不与E、F重合![]() ,对于M的每一个位置,记
,对于M的每一个位置,记![]() 的外接圆面积与
的外接圆面积与![]() 的外接圆面积的比值为
的外接圆面积的比值为![]() ,那么
,那么![]()
![]()

A. ![]() 先变小再变大
先变小再变大
B. 仅当M为线段EF的中点时,![]() 取得最大值
取得最大值
C. ![]() 先变大再变小
先变大再变小
D. ![]() 是一个定值
是一个定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 是椭圆
是椭圆![]() 上的一点,从原点
上的一点,从原点![]() 向圆
向圆![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() .
.
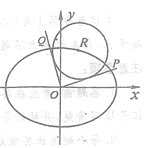
(1)若![]() 点在第一象限,且直线
点在第一象限,且直线![]() 互相垂直,求圆
互相垂直,求圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
作物产量(kg) | 300 | 500 |
概率 | 0.5 | 0.5 |
作物市场价格(元/kg) | 6 | 10 |
概率 | 0.4 | 0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com