
【题目】下列命题中,错误的是( )
A. 在![]() 中,
中, ![]() 则
则![]()
B. 在锐角![]() 中,不等式
中,不等式![]() 恒成立
恒成立
C. 在![]() 中,若
中,若![]() ,则
,则![]() 必是等腰直角三角形
必是等腰直角三角形
D. 在![]() 中,若
中,若![]() ,
, ![]() ,则
,则![]() 必是等边三角形
必是等边三角形
【答案】C
【解析】
根据三角函数的性质,正弦定理,余弦定理,结合三角形的内角关系,依次判断即可.
A. 在△ABC中,由正弦定理可得 ![]() , ∴sinA>sinBa>bA>B,因此A>B是sinA>sinB的充要条件,故A正确;
, ∴sinA>sinBa>bA>B,因此A>B是sinA>sinB的充要条件,故A正确;
B.在锐角△ABC中,A,B![]() ,且
,且![]() ,则
,则![]() ,所以
,所以
![]() ,故B正确;
,故B正确;
C.在△ABC中,由acosA=bcosB,利用正弦定理可得:sin2A=sin2B,得到2A=2B或2A=2π-2B,故A=B或![]() ,即
,即![]() 是等腰三角形或直角三角形,故C错误;
是等腰三角形或直角三角形,故C错误;
D. 在△ABC中,若B=60°,b2=ac,由余弦定理可得:b2=a2+c2-2accosB,∴ac=a2+c2-ac,即(a-c)2=0,解得a=c,又B=60°,∴△ABC必是等边三角形,故D正确;
故选C


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线l1:y=![]() x,l2:y=-
x,l2:y=-![]() x,动点P,Q分别在l1,l2上移动,|PQ|=2
x,动点P,Q分别在l1,l2上移动,|PQ|=2![]() ,N是线段PQ的中点,记点N的轨迹为曲线C.
,N是线段PQ的中点,记点N的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)过点M(0,1)分别作直线MA,MB交曲线C于A,B两点,设这两条直线的斜率分别为k1,k2,且k1+k2=2,证明:直线AB过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f (x)=lnx-x+1.
(1)求f (x)的极值;
(2)若0<a<1,证明:函数g (x)=(x-a)ex-![]() ax2+a(a-1) x(x>lna)有极小值点x0,且g (x0)<0.
ax2+a(a-1) x(x>lna)有极小值点x0,且g (x0)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且
,且![]() 时有
时有![]() ,甲、乙、丙、丁四位同学有下列结论:
,甲、乙、丙、丁四位同学有下列结论:
甲:![]() ;
;
乙:函数![]() 在
在![]() 上是增函数;
上是增函数;
丙:函数![]() 关于直线
关于直线![]() 对称;
对称;
丁:若![]() ,则关于
,则关于![]() 的方程
的方程![]() 在
在![]() 上所有根之和为
上所有根之和为![]() .
.
其中正确的是( )
A.乙、丁B.乙、丙C.甲、乙、丙D.乙、丙、丁
查看答案和解析>>
科目:高中数学 来源: 题型:
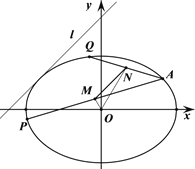
【题目】已知定直线![]() ,定点
,定点![]() ,以坐标轴为对称轴的椭圆
,以坐标轴为对称轴的椭圆![]() 过点
过点![]() 且与
且与![]() 相切.
相切.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)椭圆的弦![]() 的中点分别为
的中点分别为![]() ,若
,若![]() 平行于
平行于![]() ,则
,则![]() 斜率之和是否为定值? 若是定值,请求出该定值;若不是定值请说明理由.
斜率之和是否为定值? 若是定值,请求出该定值;若不是定值请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 定义域为
定义域为![]() ,对于区间
,对于区间![]() ,如果存在
,如果存在![]() ,
,![]() ,使得
,使得![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的区间.
的区间.
(Ⅰ)判断![]() 是否是函数
是否是函数![]() 的区间;
的区间;
(Ⅱ)若![]() 是函数
是函数![]() (其中
(其中![]() )的区间,求
)的区间,求![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() 为正实数,若
为正实数,若![]() 是函数
是函数![]() 的区间,求
的区间,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面
B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行
C.平行于同一条直线的两个平面平行
D.若直线a,b和平面α满足a∥b,a∥α,b不在平面α内,则b∥α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com