
【题目】已知抛物线![]() 过点
过点![]()
(1)求抛物线![]() 的方程,并求其焦点坐标与准线方程;
的方程,并求其焦点坐标与准线方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() 过点
过点![]() 作
作![]() 轴的垂线分别与直线
轴的垂线分别与直线![]() ,
,![]() 交于
交于![]() ,
,![]() 两点,其中
两点,其中![]() 为坐标原点.若
为坐标原点.若![]() 为线段
为线段![]() 的中点,求证:直线
的中点,求证:直线![]() 恒过定点.
恒过定点.
【答案】(1)抛物线![]() 的方程为
的方程为![]() ,其焦点坐标为
,其焦点坐标为![]() ,准线方程为
,准线方程为![]() (2)证明见解析;
(2)证明见解析;
【解析】
(1) 点![]() 代入求得
代入求得![]() ,即可的抛物线方程求得结果.
,即可的抛物线方程求得结果.
(2) 由题意知直线![]() 斜率存在且不为零,设直线
斜率存在且不为零,设直线![]() 方程为
方程为![]() ,与抛物线方程联立,设
,与抛物线方程联立,设![]() ,
,![]() ,根据已知由
,根据已知由![]() :
:![]() ,
, ![]() :
:![]() ,及过点
,及过点![]() 作
作![]() 轴的垂线求得
轴的垂线求得![]() 的坐标,根据
的坐标,根据![]() 为线段
为线段![]() 的中点,借助韦达定理化简即可证得结论.
的中点,借助韦达定理化简即可证得结论.
解:(1)由抛物线![]() 过点
过点![]() ,
,
得![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() ,
,
其焦点坐标为![]() ,准线方程为
,准线方程为![]() .
.
(2)由题意知直线![]() 斜率存在且不为零,设直线
斜率存在且不为零,设直线![]() 方程为
方程为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 的交点为
的交点为![]() ,
,![]() .
.
由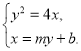 得
得![]() ,
,
由韦达定理,得![]() ,
,![]() .
.
由已知得直线![]() 的方程为
的方程为![]() ,所以
,所以![]() ,
,
由已知得直线![]() 方程为
方程为![]() ,所以
,所以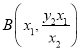 .
.
因为![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() ①,
①,
将![]() ,
,![]() ,代入①式,并化简得
,代入①式,并化简得![]() ,
,
把![]() ,
,![]() 代入②式,化简得
代入②式,化简得![]()
所以直线![]() 的方程为
的方程为![]() ,故直线
,故直线![]() 恒过定点
恒过定点![]() .
.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() 是圆O的直径,点C是圆O上异于A,B的点,直线
是圆O的直径,点C是圆O上异于A,B的点,直线![]() 平面
平面![]() ,E,F分别是
,E,F分别是![]() ,
,![]() 的中点.
的中点.

(1)记平面![]() 与平面
与平面![]() 的交线为l,试判断直线l与平面
的交线为l,试判断直线l与平面![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)设![]() ,求二面角
,求二面角![]() 大小的取值范围.
大小的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为
为![]() 上的动点,
上的动点,![]() 为
为![]() 的中点.
的中点.
(1)请求出![]() 点轨迹
点轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() 若直线
若直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() ,弦
,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正六棱锥![]() 中,底面边长和侧棱分别是2和4,
中,底面边长和侧棱分别是2和4,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,给出下面三个判断:(1)
的中点,给出下面三个判断:(1)![]() 和
和![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;(2)
;(2)![]() 和底面所成的角是
和底面所成的角是![]() ;(3)平面
;(3)平面![]() 平面
平面![]() ;其中判断正确的个数是( )
;其中判断正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为![]() .
.
(1)设椭圆的左右焦点分别为![]() 、
、![]() ,点
,点![]() 在椭圆上运动,求
在椭圆上运动,求![]() 的值;
的值;
(2)设直线![]() 和圆
和圆![]() 相切,和椭圆交于
相切,和椭圆交于![]() 、
、![]() 两点,
两点,![]() 为原点,线段
为原点,线段![]() 、
、![]() 分别和圆
分别和圆![]() 交于
交于![]() 、
、![]() 两点,设
两点,设![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的逐步提高,人们对文娱活动的需求与日俱增,其中观看电视就是一种老少皆宜的娱乐活动.但是我们在观看电视娱乐身心的同时,也要注意把握好观看时间,近期研究显示,一项久坐的生活指标——看电视时间,是导致视力下降的重要因素,即看电视时间越长,视力下降的风险越大.研究者在某小区统计了每天看电视时间![]() (单位:小时)与视力下降人数
(单位:小时)与视力下降人数![]() 的相关数据如下:
的相关数据如下:
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
(1)请根据上面的数据求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(2)我们用(1)问求出的线性回归方程![]() 的
的![]() 估计回归方程
估计回归方程![]() ,由于随机误差
,由于随机误差![]() ,所以
,所以![]() 是
是![]() 的估计值,
的估计值,![]() 成为点(
成为点(![]() ,
,![]() )的残差.
)的残差.
①填写下面的残差表,并绘制残差图;
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
|
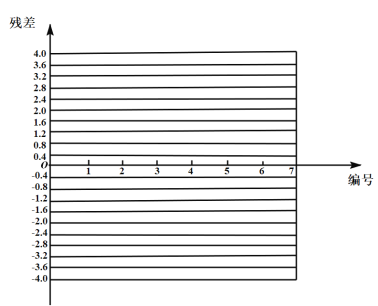
②若残差图所在带状区域宽度不超过4,我们则认为该模型拟合精度比较高,回归方程的预报精度较高,试根据①绘制的残差图分折该模型拟合精度是否比较高?
附:回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为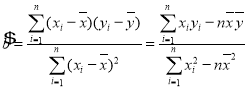 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称粽子,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期的楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为2的正三角形组成的,将它沿虚线对折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______________
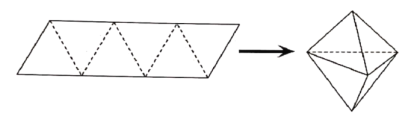
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率π是数学中一个非常重要的数,历史上许多中外数学家利用各种办法对π进行了估算.现利用下列实验我们也可对圆周率进行估算.假设某校共有学生N人,让每人随机写出一对小于1的正实数a,b,再统计出a,b,1能构造锐角三角形的人数M,利用所学的有关知识,则可估计出π的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某地区打算在一块矩形地块上修建一个牧场(ABCDEF围成的封闭区域)用来养殖牛和羊,其中AF=1,AB=10,BC=4,CD=7(单位:百米),DEF是一段曲线形马路.该牧场的核心区为等腰直角三角形MPQ所示区域,该区域用来养殖羊,其余区域养殖牛,且MP=PQ,牧场大门位于马路DEF上的M处,一个观察点P位于AB的中点处,为了能够更好观察动物的生活情况,现决定修建一条观察通道,起点位于距离观察点P处1百米的O点所示位置,终点位于Q处.如图2所示,建立平面直角坐标系,若![]() 满足
满足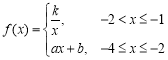 .
.
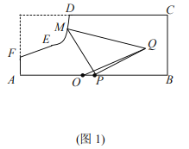
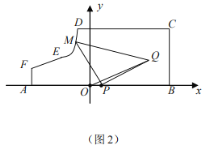
(1)求![]() 的解析式;
的解析式;
(2)求观察通道OQ长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com