练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4:坐标系与参数方程

    在平面直角坐标系中，直线经过点，倾斜角为.在以原点为极点， 轴正半轴为极轴的极坐标系中，曲线的方程为.

    （1）写出直线的参数方程和曲线的直角坐标方程；

    （2）设直线与曲线相交于两点，求的值.

    【答案】（1）直线的参数方程为 (为参数）；曲线的直角坐标方程为；（2）．

    【解析】试题分析：（1）先根据直线参数方程标准式写直线的参数方程，利用化简极坐标方程为直角坐标方程；（2）将直线参数方程代入圆方程，再根据参数几何意义化简，最后根据韦达定理代入化简求值

    试题解析：（1）直线的参数方程为 (为参数）.

    ∵，∴，∴，即，

    故曲线的直角坐标方程为.

    （2）将的参数方程代入曲线的直角坐标方程，得，

    显然, ∴, ∴，

    ，

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设向量 =（ sinx，sinx）， =（cosx，sinx），x∈[0， ]．
    （1）若| |=| |，求x的值；
    （2）设函数f（x）= ，求f（x）的最大值及单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣x﹣ （x＜0），g（x）=x2+bx﹣2（x＞0），b∈R，若f（x）图象上存在A，B两个不同的点与g（x）图象上A′，B′两点关于y轴对称，则b的取值范围为（ ）
    A.（﹣4 ﹣5，+∞）
    B.（4 ﹣5，+∞）
    C.（﹣4 ﹣5，1）
    D.（4 ﹣5，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= （x＞0）．
    （1）试判断函数f（x）在（0，+∞）上单调性并证明你的结论；
    （2）若f（x）＞ 恒成立，求整数k的最大值；
    （3）求证：（1+1×2）（1+2×3）…[1+n（n+1）]＞e2n﹣3 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形与均为菱形， ，且.

    （1）求证： 平面；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，E，F分别为PA，BD中点，PA=PD=AD=2．
    （Ⅰ）求证：EF∥平面PBC；
    （Ⅱ）求二面角E﹣DF﹣A的余弦值；
    （Ⅲ）在棱PC上是否存在一点G，使GF⊥平面EDF？若存在，指出点G的位置；若不存在，说明理由．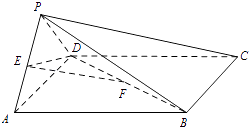

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若等比数列{an}的前n项和Sn=2016n+t（t为常数），则a1的值为（ ）
    A.2013
    B.2014
    C.2015
    D.2016

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在上的函数满足:函数的图象关于直线对称,且当时是函数的导函数)成立.若,则的大小关系是

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知平面直角坐标系，以为极点， 轴的非负半轴为极轴建立极坐标系， 点的极坐标为，曲线的参数方程为（为参数）.

    （1）写出点的直角坐标及曲线的直角坐标方程；

    （2）若为曲线上的动点，求的中点到直线： 的距离的最小值.

    查看答案和解析>>

    同步练习册答案