
已知函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .
.
(Ⅰ)已知函数 ,
, ,判断
,判断 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(Ⅱ)已知函数 若
若 具有性质
具有性质 ,求
,求 的最大值;
的最大值;
(Ⅲ)若函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足 ,
,
求证:对任意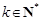 且
且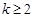 ,函数
,函数 具有性质
具有性质 .
.
(Ⅰ)具有该性质,证明见解析;(Ⅱ) ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】
试题分析:(Ⅰ)创新定义问题,首先要读懂具有性质P(m)的意思, 对于给定的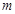 (
( 且
且 ),
),
存在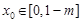 ,使得
,使得 ,按照此定义进行判断,假设具有该性质, 设
,按照此定义进行判断,假设具有该性质, 设 ,令
,令
 ,解得
,解得
 ,满足定义,故具有性质P(3);(Ⅱ)m在0到1之间,取一半,看是
,满足定义,故具有性质P(3);(Ⅱ)m在0到1之间,取一半,看是
否具有性质P( ),如果有,再判断是否有大于
),如果有,再判断是否有大于 的m,没有的话,最大值就是
的m,没有的话,最大值就是 ;(Ⅲ)构造函数
;(Ⅲ)构造函数
 ,
, 则
则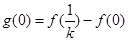 ,
, …
… …
… =
=
 -
- ,相加,有
,相加,有 ,分里面有零和没零进行讨论,得到结论.
,分里面有零和没零进行讨论,得到结论.
试题解析:(Ⅰ)设 ,即
,即
令 , 则
, 则
解得
 ,
,
所以函数 具有性质
具有性质
(Ⅱ)m的最大值为 .
.
首先当 时,取
时,取 ,
,
则 ,
, ,
,
所以函数 具有性质
具有性质 ,
,
假设存在 ,使得函数
,使得函数 具有性质
具有性质 ,
,
则 ,
,
当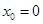 时,
时, ,
, ,
, ,
,
当 时,
时, ,
, ,
, ,
,
所以不存在 ,使得
,使得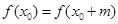 ,
,
故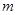 的最大值为
的最大值为 .
.
(Ⅲ)任取 ,
,
设 ,其中
,其中 ,
,
 则有
则有
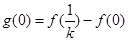
 ,
,
 ,
,
……
 ,
,
……
 ,
,
以上各式相加得: ,
,
当 中有一个为
中有一个为 时,不妨设为
时,不妨设为 ,
,
即 ,
,
则函数 具有性质
具有性质 ,
,
当 均不为
均不为 时,由于其和为
时,由于其和为 ,则必然存在正数和负数,
,则必然存在正数和负数,
不妨设 其中
其中 ,
, ,
,
由于 是连续的,所以当
是连续的,所以当 时,至少存在一个
时,至少存在一个 ,
,
(当 时,至少存在一个
时,至少存在一个 ),
),
使得 ,
,
即 ,
,
故函数 具有性质
具有性质 .
.
考点:1.抽象函数的定义;2.创新问题情境;3.构造函数.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省杭州市七校高三上学期期中联考理科数学试卷(解析版) 题型:解答题
已知函数 的定义域为
的定义域为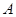 ,
,
(1)求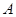 ;
;
(2)若 ,且
,且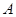 是
是 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届辽宁朝阳高二下学期期中考试理科数学试卷(解析版) 题型:选择题
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
查看答案和解析>>
科目:高中数学 来源:2010-2011学年海南省海口市高三高考调研考试理科数学 题型:选择题
已知函数 的定义域为
的定义域为 ,且
,且 ,
, 为
为 的导函数,函数
的导函数,函数 的图象如图所示.若正数
的图象如图所示.若正数 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是

A.  B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com