练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆：（）过点与.

    （1）求椭圆的方程；

    （2）设过椭圆的右焦点，且倾斜角为的直线和椭圆交于、两点，对于椭圆上任一点，若，求的最大值.

    【答案】（1）（2）

    【解析】

    （1）把已知点的坐标代入椭圆方程，得到关于，的方程组，求解可得，的值，则椭圆的方程可求；

    （2）由（1）知，，，由题意可知的方程，与椭圆方程联立，化为关于的一元二次方程，由，，在椭圆上及根与系数的关系可得，再由基本不等式求最值．

    解：（1）∵椭圆过点与，∴，.

    ∴，，∴椭圆的方程为.

    （2）由（1）知，由题意可知的方程为，①

    椭圆的方程可化为，②

    将①代入②消去，得，③

    设，，则有，，

    设，由得，

    ∴又点在椭圆上，

    ∴

    ，④

    又，在椭圆上，故有，，⑤

    而

    ，⑥

    将⑤⑥代入④可得，

    ∵，

    ∴，当且仅当时取“=”，则的最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设为平面直角坐标系xOy中的点集，从中的任意一点P作x轴、y轴的垂线，垂足分别为M,N,记点M的横坐标的最大值与最小值之差为x(),点N的纵坐标的最大值与最小值之差为y().若是边长为1的正方形，给出下列三个结论:

    ①x(Q)的最大值为

    ②x(Q)+y(Q)的取值范围是

    ③x(Q)-y(Q)恒等于0.

    其中所有正确结论的序号是_________

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为，Q为l上的动点，以OQ为边作等边三角形OPQ，且三点O，P，Q按逆时针方向排列.

    （Ⅰ）设点P运动轨迹E的直角坐标方程；

    （Ⅱ）若曲线经过伸缩变换得到曲线，若点M为曲线上的动点，且点M到曲线E的最小距离为1，求实数a的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于集合，，，，定义.

    集合中的元素个数记为，当，称集合具有性质.

    （1）已知集合，，写出，的值，并判断集合是否具有性质；

    （2）设集合具有性质，判断集合中的三个元素是否能组成等差数列，请说明理由；

    （3）若数列是以为首项，2为公比的等比数列. 数列中的前100项：组成的集合记作，将集合中的所有元素从小到大排序，即满足，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着夏季的到来，冰枕成为市面上的一种热销产品，某厂家为了调查冰枕在当地大学的销售情况，作出调研，并将所得数据统计如下表所示：

    表一：

    温度在30℃以下

    温度在30℃以上

    总计

    女生

    10

    30

    40

    男生

    40

    20

    60

    总计

    50

    50

    100

    随后在该大学一个小卖部调查了冰枕的出售情况，并将某月的日销售件数（x）与销售天数（y）统计如下表所示：

    表二：

    第天

    2

    4

    6

    8

    10

    （件）

    3

    6

    7

    10

    12

    （1）请根据表二中的数据在下列网格纸中绘制散点图；

    （2）请根据表二中提供的数据，用最小二乘法求出y关于x的线性回归方程；

    （3）从（1）（2）中的数据及回归方程我们可以得到，销售件数随着销售天数的增长而增长，但无法判断男、女生对冰枕的选择是否与温度有关，请结合表一中的数据，并自己设计方案来判段是否有99.9%的可能性说明购买冰枕的性别与温度相关.

    参考数据及公式：

    P(K2≥k0)

    0.100

    0.050

    0.025

    0.010

    0.005

    0.001

    k0

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

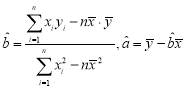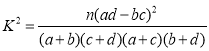    ；，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，矩形中， ， ，点是上的动点．现将矩形沿着对角线折成二面角，使得．

    （Ⅰ）求证：当时， ；

    （Ⅱ）试求的长，使得二面角的大小为．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）当时，求曲线在处的切线方程；

    （2）当时，求函数的最小值；

    （3）已知，且任意有，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，点的极坐标为，直线的极坐标方程为，且过点，曲线的参数方程为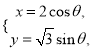 (为参数).

    (Ⅰ)求曲线上的点到直线的距离的最大值；

    (Ⅱ)过点与直线平行的直线与曲线 交于两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国古代儒家要求学生掌握六种基本才艺：礼、乐、射、御、书、数，简称“六艺”,某高中学校为弘扬“六艺”的传统文化，分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛，现有甲、乙、丙三位选手进入了前三名的最后角逐,规定：每场知识竞赛前三名的得分都分别为且；选手最后得分为各场得分之和，在六场比赛后，已知甲最后得分为分，乙和丙最后得分都是分，且乙在其中一场比赛中获得第一名，下列说法正确的是( )

    A. 乙有四场比赛获得第三名

    B. 每场比赛第一名得分为

    C. 甲可能有一场比赛获得第二名

    D. 丙可能有一场比赛获得第一名

    查看答案和解析>>

    同步练习册答案