
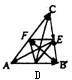
 点D,E,F分别是△ABC三边AB,BC,CA的中点,求证:
点D,E,F分别是△ABC三边AB,BC,CA的中点,求证:| AB |
| BE |
| AC |
| CE |
| EA |
| FB |
| DC |
| 0 |
| EA |
| FB |
| DC |
| 0 |
| AB |
| BE |
| AE |
| AC |
| CE |
| AE |
| AB |
| BE |
| AC |
| CE |
| EA |
| EB |
| BA |
| FB |
| FC |
| CB |
| DC |
| DB |
| BC |
| EA |
| FB |
| DC |
| EB |
| BA |
| FC |
| CB |
| DB |
| BC |
| EB |
| BA |
| FC |
| DB |
| FC |
| AF |
| EB |
| BF |
| DB |
| EF |
| DB |
| EF |
| BD |
| 0 |


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
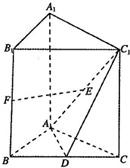 19、如图,在正三棱柱ABC-A1B1C1中,点D、E、F分别是BC、AC1、BB1的中点.
19、如图,在正三棱柱ABC-A1B1C1中,点D、E、F分别是BC、AC1、BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
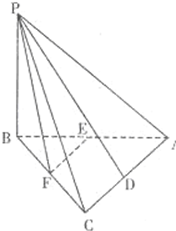 (2012•广安二模)如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点.
(2012•广安二模)如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点.查看答案和解析>>
科目:高中数学 来源:2010年河南省许昌市六校联考高一下学期期末考试数学卷 题型:选择题
已知点D、E、F分别是△ABC的边BC、CA、AB的中点,且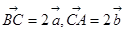 ,给出下列四个等式:①
,给出下列四个等式:①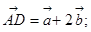 ②
②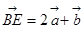 ;
;
③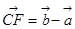 ;④
;④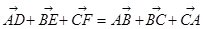 .
.
其中正确命题的序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com