
分析 (1)举出反例即可,只要检验f(-1)≠-f(1),可说明f(x)不是奇函数;
(2)由题意可得f(-x)=-f(x),即$\frac{-{2}^{-x}+1}{{2}^{-x+1}+b}$=-$\frac{-{2}^{x}+a}{{2}^{x+1}+b}$对定义域内任意实数x成立.整理可求a,b
(3)当$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$时,f(x)=-$\frac{1}{2}$+$\frac{1}{{2}^{x}+1}$,由指数函数的性质可求f(x),由二次函数的性质可求c2-3c+3=(c-$\frac{3}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,当$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$时,f(x)=-$\frac{1}{2}$+$\frac{1}{1-{2}^{x}}$(x≠0),当x>0时,f(x)<-$\frac{1}{2}$;当x<0时,f(x)>$\frac{1}{2}$结合二次函数的性质可求c2-3c+3的范围,即可求解.
解答 (1)证明:当a=b=1时,f(1)=-$\frac{1}{5}$,f(-1)=$\frac{1}{4}$
所以f(-1)≠-f(1),
所以f(x)不是奇函数;(4分)
(2)解:f(x)是奇函数时,f(-x)=-f(x),即$\frac{-{2}^{-x}+1}{{2}^{-x+1}+b}$=-$\frac{-{2}^{x}+a}{{2}^{x+1}+b}$对定义域内任意实数x成立.(1分)
化简整理得(2a-b)•22x+(2ab-4)•2x+(2a-b)=0,这是关于x的恒等式,
所以$\left\{\begin{array}{l}{2a-b=0}\\{2ab-4=0}\end{array}\right.$,
所以$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$或$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$.
经检验都符合题意.(3分)
(3)解:当$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$时,f(x)=-$\frac{1}{2}$+$\frac{1}{{2}^{x}+1}$,
因为2x>0,
所以2x+1>1,0<$\frac{1}{{2}^{x}+1}$<1,从而-$\frac{1}{2}<f(x)<\frac{1}{2}$;(2分)
而c2-3c+3=(c-$\frac{3}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$对任何实数c成立;
所以可取D=R对任何x、c属于D,都有f(x)<c2-3c+3成立.(3分)
当$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$时,f(x)=-$\frac{1}{2}$+$\frac{1}{1-{2}^{x}}$(x≠0),
所以当x>0时,f(x)<-$\frac{1}{2}$;当x<0时,f(x)>$\frac{1}{2}$; (2分)
①因此取D=(0,+∞),对任何x、c属于D,都有f(x)<c2-3c+3成立.(1分)
②当c<0时,c2-3c+3>3,解不等式-$\frac{1}{2}$+$\frac{1}{1-{2}^{x}}$≤3得:x≤$lo{g}_{2}\frac{5}{7}$.
所以取D=(-∞,$lo{g}_{2}\frac{5}{7}$],对任何属于D的x、c,都有f(x)<c2-3c+3成立. (2分)
点评 本题主要考查了函数的奇偶性的判断,及奇函数性质的应用,指数函数、二次函数性质的综合应用是解答本题的关键


科目:高中数学 来源: 题型:选择题
| A. | 共面 | B. | 不共面 | C. | 共线 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 180 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}-\sqrt{2}}{6}$ | B. | -$\frac{\sqrt{2}}{3}$-$\frac{1}{6}$ | C. | $\frac{1}{2}$-$\frac{\sqrt{3}}{6}$ | D. | -$\frac{\sqrt{6}}{3}$-$\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
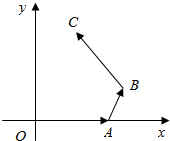 如图,在平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}=(-1,\sqrt{3})$,求点B,C的坐标.
如图,在平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}=(-1,\sqrt{3})$,求点B,C的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com