
已知{an}是正数组成的数列,a1=1,且点(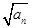 ,an+1)( n ∈N*)在函数y=x2+1的图象上.
,an+1)( n ∈N*)在函数y=x2+1的图象上.
(1)求数列{an}的通项公式;
(2)若数列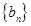 满足b1=1,
满足b1=1,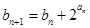 ,求证:
,求证: .
.
(1)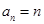 ; (2) 证明过程见试题解析.
; (2) 证明过程见试题解析.
解析试题分析:(1)将点的坐标代入函数可得an+1-an=1,知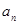 是以1为公差,1为首项的等差数列,可得通项公式;(2)由所给条件,可得
是以1为公差,1为首项的等差数列,可得通项公式;(2)由所给条件,可得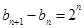 ,对n分别取值后,用累加法得出
,对n分别取值后,用累加法得出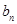 的通项公式
的通项公式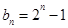 ,则
,则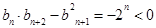 ,命题可证.
,命题可证.
解:(1) 由已知得an+1=an+1,则an+1-an=1,又a1=1,
所以数列{an}是以1为首项,1为公差的等差数列,
故an=1+(n-1)1=n. 4分
(2)由(1)知,an=n,从而 -
-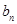 =2n.
=2n.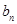 =(
=(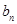 -
-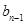 )+(
)+(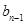 -
-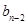 )+ +(b2-b1)+b1 ,
)+ +(b2-b1)+b1 ,
=2n-1+2n-2+ +2+1= =
=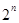 -1.
-1.
因为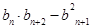 =(2n-1)(2n+2-1)-(2n+1-1)2
=(2n-1)(2n+2-1)-(2n+1-1)2
=(22n+2-2n+2-2n+1)-(22n+2-2·2n+1+1),
=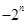 <0,
<0,
所以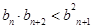 . 12分
. 12分
考点:等差数列的通项公式.累加法求数列的通项公式.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
已知公差不为0的等差数列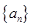 满足
满足 ,
,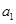 ,
,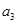 ,
,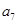 成等比数列.
成等比数列.
(1)求数列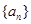 的通项公式;(2)数列
的通项公式;(2)数列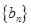 满足
满足 ,求数列
,求数列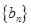 的前
的前 项和
项和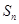 ;(Ⅲ)设
;(Ⅲ)设 ,若数列
,若数列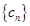 是单调递减数列,求实数
是单调递减数列,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)(2011•湖北)成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+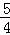 }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知实数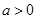 ,且
,且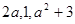 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求实数 的值;
的值;
(2)若等差数列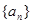 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列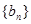 的首项和公比都为
的首项和公比都为 ,数列
,数列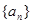 和
和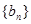 的前
的前 项和分别为
项和分别为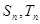 ,且
,且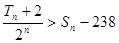 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2012•广东)设数列{an}的前n项和为Sn,满足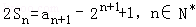 ,且a1,a2+5,a3成等差数列.
,且a1,a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有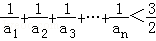 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
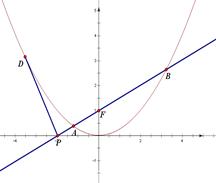
抛物线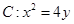 ,直线
,直线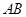 过抛物线
过抛物线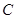 的焦点
的焦点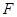 ,交
,交 轴于点
轴于点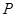 .
.
(1)求证: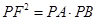 ;
;
(2)过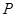 作抛物线
作抛物线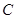 的切线,切点为
的切线,切点为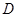 (异于原点),
(异于原点),
(ⅰ)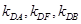 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ⅱ)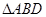 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com